题目内容
17．已知复数z1=3-i，z2=1+i，$\overline{{z}_{1}}$是z1的共轭复数，则$\frac{\overline{{z}_{1}}}{{z}_{2}}$=（ ）| A． | 1+i | B． | 1-i | C． | 2+i | D． | 2-i |
分析 由已知求出$\overline{{z}_{1}}$，代入$\frac{\overline{{z}_{1}}}{{z}_{2}}$，然后利用复数代数形式的乘除运算化简得答案．
解答 解：∵z1=3-i，z2=1+i，
∴$\overline{{z}_{1}}$=3+i，
则$\frac{\overline{{z}_{1}}}{{z}_{2}}$=$\frac{3+i}{1+i}=\frac{（3+i）（1-i）}{（1+i）（1-i）}=\frac{4-2i}{2}=2-i$．
故选：D．
点评 本题考查复数代数形式的乘除运算，是基础的计算题．
练习册系列答案
相关题目
2．函数y=$\frac{2}{\sqrt{x-4}}$的值域是（ ）
| A． | R | B． | （0，+∞） | C． | （-∞，4） | D． | （-∞，4）∪（4，+∞） |
5．下列函数中是偶函数，且又在区间（-∞，0）上是增函数的是（ ）
| A． | y=x2 | B． | y=x-2 | C． | $y={（\frac{1}{4}）^{-|x|}}$ | D． | $y={log_3}{x^{\frac{5}{6}}}$ |
12．设F1、F2分别是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左、右焦点，若椭圆上存在点A，使∠F1AF2=90°，且|AF1|=3|AF2|，则椭圆离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{4}$ | B． | $\frac{{\sqrt{10}}}{4}$ | C． | $\frac{{\sqrt{15}}}{4}$ | D． | $\sqrt{5}$ |
一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于2．
9．已知$A=\{x||{x-2}|＜1\}，B=\{y|y=\frac{2x-1}{x+1}，x∈A\}$，则A∩B=（ ）
| A． | $（\frac{1}{2}，\frac{5}{4}）$ | B． | $（\frac{7}{4}，3）$ | C． | $（1，\frac{5}{4}）$ | D． | $（\frac{1}{2}，1）$ |
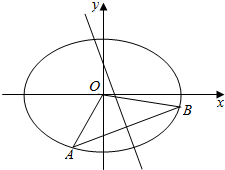已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A，B关于直线$y=mx+\frac{1}{2}（m≠0）$对称．