题目内容
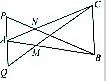 在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量
在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量| AB |
| a |
| AC |
| b |
(1)用向量
| a |
| b |
| AP |
(2)用向量知识证明:A、P、Q三点共线,且AP=AQ.
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由题意,连结MN作图,由相似比可出求λ的值.
解答:
 解:(1)由AC=3AN,AB=3AM,BN=2NP,得到MN∥BC∥AP,向量
解:(1)由AC=3AN,AB=3AM,BN=2NP,得到MN∥BC∥AP,向量
=
+
=
+
=
+
-
,所以
=
-
,所以
=
-
;
(2)在CM的延长线上取点Q,使CM=2MQ,又AC=3AN,所以MN∥AQ,所以
=
+
=
+
=
+
-
,所以
=
-
,
所以
=
-
,
所以
=-
,
所以A、P、Q三点共线,且AP=AQ.
 解:(1)由AC=3AN,AB=3AM,BN=2NP,得到MN∥BC∥AP,向量
解:(1)由AC=3AN,AB=3AM,BN=2NP,得到MN∥BC∥AP,向量| AP |
| AN |
| NP |
| 1 |
| 3 |
| AC |
| 1 |
| 3 |
| BP |
| 1 |
| 3 |
| AC |
| 1 |
| 3 |
| AP |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AP |
| 1 |
| 3 |
| b |
| 1 |
| 3 |
| a |
| AP |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| a |
(2)在CM的延长线上取点Q,使CM=2MQ,又AC=3AN,所以MN∥AQ,所以
| AQ |
| AM |
| MQ |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| CQ |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| AQ |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| AQ |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
所以
| AQ |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
所以
| AQ |
| AP |
所以A、P、Q三点共线,且AP=AQ.
点评:本题考查了平面向量的应用及平面几何中相似比的应用,属于中档题.

练习册系列答案
相关题目
双曲线
-
=1的左右焦点分别为F1,F2,点P为该双曲线在第一像限的点,△PF1F2的面积为1,且tan∠PF1F2=0.5,tan∠PF2F1=-2,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、3x2-
| ||||
D、
|
线段AB长为2a,两端点A,B分别在一个直二面角的两个面内,且AB与两个面所成的角分别为30°和45°,设A,B两点在二面角棱上的射影分别为A′,B′,则A′B′的长为( )
A、
| ||||
B、
| ||||
| C、a | ||||
| D、2a |
设
、
是平面内的两个向量,则有( )
| e1 |
| e2 |
A、
| ||||||||||||
B、
| ||||||||||||
C、对同一平面内的任一向量
| ||||||||||||
D、若
|
定义域为R的函数f(x),对?x都有f(x)=f(2-x),则下列选项一定正确的是( )
| A、f(-x)为偶函数 |
| B、f(x-1)为偶函数 |
| C、f(1-x)为偶函数 |
| D、f(x-2)为偶函数 |