题目内容
双曲线
-
=1的左右焦点分别为F1,F2,点P为该双曲线在第一像限的点,△PF1F2的面积为1,且tan∠PF1F2=0.5,tan∠PF2F1=-2,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、3x2-
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,三角函数的求值,圆锥曲线的定义、性质与方程
分析:运用同角公式,求出sin∠F1PF2=
,cos∠F1PF2=-
,sin∠PF1F2=
,sin∠PF2F1=
,再由面积公式,可得PF1•PF2=
,再由余弦定理,可得b2=3,即c2-a2=3,①再由正弦定理,可得e=
=
,②求得a2=
,进而得到双曲线的方程.
| 3 |
| 5 |
| 4 |
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| 10 |
| 3 |
| c |
| a |
| 3 | ||
|
| 15 |
| 4 |
解答:
解:在△PF1F2中,tan∠F1PF2=-tan(∠PF1F2+∠PF2F1)
=-
=-
.由
=-
.及sin2∠F1PF2+cos2∠F1PF2=1,
可得,sin∠F1PF2=
,cos∠F1PF2=-
,
由于△PF1F2的面积为1,则
PF1•PF2•sin∠F1PF2=1,即有PF1•PF2=
,
cos∠F1PF2=
=
+1=
+1=-
,
即有b2=3,即c2-a2=3,①
由于tan∠PF1F2=0.5,tan∠PF2F1=-2,可得,sin∠PF1F2=
,sin∠PF2F1=
,
由正弦定理,可得,
=
=
,
即有
=
=
,即有e=
=
,②
①②解得,a2=
,
则该双曲线的方程为
-
=1.
故选B.
=-
| ||
1-
|
| 3 |
| 4 |
| sin∠F1PF2 |
| cos∠F1PF2 |
| 3 |
| 4 |
可得,sin∠F1PF2=
| 3 |
| 5 |
| 4 |
| 5 |
由于△PF1F2的面积为1,则
| 1 |
| 2 |
| 10 |
| 3 |
cos∠F1PF2=
| PF12+PF22-F1F22 |
| 2PF1•PF2 |
| (PF1-PF2)2-4c2 |
| 2PF1•PF2 |
| 2(a2-c2) |
| PF1•PF2 |
| 4 |
| 5 |
即有b2=3,即c2-a2=3,①
由于tan∠PF1F2=0.5,tan∠PF2F1=-2,可得,sin∠PF1F2=
| ||
| 5 |
2
| ||
| 5 |
由正弦定理,可得,
| PF1 |
| sin∠PF2F1 |
| PF2 |
| sin∠PF1F2 |
| F1F2 |
| sin∠F1PF2 |
即有
| PF1-PF2 | ||||
|
| 2a | ||||
|
| 2c | ||
|
| c |
| a |
| 3 | ||
|
①②解得,a2=
| 15 |
| 4 |
则该双曲线的方程为
| 4x2 |
| 15 |
| y2 |
| 3 |
故选B.
点评:本题考查双曲线的定义、方程和性质,考查正弦定理、余弦定理和面积公式的运用,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
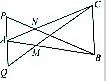 在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量
在△ABC中,在AC上取点N,使AC=3AN,在AB上取点M,使AB=3AM,在BN的延长线上取点P,使BN=2NP,在CM的延长线上取点Q,使CM=2MQ,如图所示,记向量