题目内容
已知函数f（x）=
的定义域为A，函数g（x）=2x（-1≤x≤m）的值域为B．
（1）当m=1时，求A∩B；
（2）若A∩B=A，求实数m的取值范围．
| log0.5(4x-3) |
（1）当m=1时，求A∩B；
（2）若A∩B=A，求实数m的取值范围．
考点：交集及其运算,集合的包含关系判断及应用
专题：集合
分析：（1）求函数f（x）=
的定义域可得A=（
，1]，当m=1时，求函数g（x）=2x的值域，可得B，进而根据集合交集的定义，可得A∩B；
（2）若A∩B=A，可得：A⊆B，结合A=（
，1]，可得：1≤2m，解得实数m的取值范围．
| log0.5(4x-3) |
| 3 |
| 4 |
（2）若A∩B=A，可得：A⊆B，结合A=（
| 3 |
| 4 |
解答：
解：（1）由0＜4x-3≤1得：x∈（
，1]，
故A=（
，1]，
当m=1时，g（x）=2x∈[
，2]，
即B=[
，2]，
∴A∩B=（
，1]，
（2）∵A∩B=A，
∴A⊆B，
又∵A=（
，1]，
∴1≤2m，
解得：m≥0
| 3 |
| 4 |
故A=（
| 3 |
| 4 |
当m=1时，g（x）=2x∈[
| 1 |
| 2 |
即B=[
| 1 |
| 2 |
∴A∩B=（
| 3 |
| 4 |
（2）∵A∩B=A，
∴A⊆B，
又∵A=（
| 3 |
| 4 |
∴1≤2m，
解得：m≥0
点评：本题考查的知识点是集合的交集运算，集合的包含关系，函数的定义域和值域，难度中档．
练习册系列答案
名校课堂系列答案
相关题目
下列函数中，在区间（0，+∞）上为增函数的是（ ）
| A、y=ln（x+3） | ||
B、y=-
| ||
C、y=(
| ||
D、y=
|
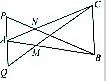在△ABC中，在AC上取点N，使AC=3AN，在AB上取点M，使AB=3AM，在BN的延长线上取点P，使BN=2NP，在CM的延长线上取点Q，使CM=2MQ，如图所示，记向量