题目内容
已知k∈R,设f(θ)=cos2θ+(k-4)sinθ+2k-9,其中θ∈[0,2π).
(1)当k=3时,求f(θ)的最值,并求相应的θ;
(2)若对任意θ∈[0,2π),f(θ)≤0恒成立,求k的取值范围;
(3)若存在唯一的θ∈[0,2π),使f(θ)≤0,求θ、k的取值.
(1)当k=3时,求f(θ)的最值,并求相应的θ;
(2)若对任意θ∈[0,2π),f(θ)≤0恒成立,求k的取值范围;
(3)若存在唯一的θ∈[0,2π),使f(θ)≤0,求θ、k的取值.
考点:同角三角函数基本关系的运用,三角函数的最值
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质,不等式的解法及应用
分析:(1)首先对函数关系是进行恒等变换然后根据自变量与对称轴的关系求出函数的最值及相应的自变量的值.
(2)f(θ)=-(sinθ-
)2+
若对任意θ∈[0,2π),f(θ)≤0恒成立,只需满足
≤0即可,进一步求出k的取值范围.
(3)存在唯一的θ∈[0,2π),使f(θ)≤0,不但在(2)的基础上,同时要满足sinθ=
,由于-1≤sinθ≤1,-1≤
≤1,求出交集即可.
(2)f(θ)=-(sinθ-
| k-4 |
| 2 |
| k2-16 |
| 4 |
| k2-16 |
| 4 |
(3)存在唯一的θ∈[0,2π),使f(θ)≤0,不但在(2)的基础上,同时要满足sinθ=
| k-4 |
| 2 |
| k-4 |
| 2 |
解答:
解:(1)∵f(θ)=cos2θ+(k-4)sinθ+2k-9,
当k=3时,f(θ)=cos2θ-sinθ-3=-(sinθ+
)2-
,
当sinθ=-
即θ=
或
时,f(θ)max=-
,
当sinθ=1时 即θ=
时,f(θ)min=-4;
(2)∵f(θ)=cos2θ+(k-4)sinθ+2k-9=-sin2θ+(k-4)sinθ+2k-8
=-(sinθ-
)2+
+2k-8=-(sinθ-
)2+
,
若对任意θ∈[0,2π),f(θ)≤0恒成立,只需满足
≤0即可,
即:-4≤k≤4;
(3)由(2)得:f(θ)=-(sinθ-
)2+
,
存在唯一的θ∈[0,2π),使f(θ)≤0,
则:sinθ=
由于-1≤sinθ≤1,
-1≤
≤1,
解得:2≤k≤6;
联立:-4≤k≤4,
∴2≤k≤4,
此时θ=arcsin
,
故答案为:(1)θ=
或
时,f(θ)max=-
,θ=
时,f(θ)min=-4;
(2)-4≤k≤4;
(3)2≤k≤4,θ=arcsin
.
当k=3时,f(θ)=cos2θ-sinθ-3=-(sinθ+
| 1 |
| 2 |
| 7 |
| 4 |
当sinθ=-
| 1 |
| 2 |
| 7π |
| 6 |
| 11π |
| 6 |
| 7 |
| 4 |
当sinθ=1时 即θ=
| π |
| 2 |
(2)∵f(θ)=cos2θ+(k-4)sinθ+2k-9=-sin2θ+(k-4)sinθ+2k-8
=-(sinθ-
| k-4 |
| 2 |
| (k-4)2 |
| 4 |
| k-4 |
| 2 |
| k2-16 |
| 4 |
若对任意θ∈[0,2π),f(θ)≤0恒成立,只需满足
| k2-16 |
| 4 |
即:-4≤k≤4;
(3)由(2)得:f(θ)=-(sinθ-
| k-4 |
| 2 |
| k2-16 |
| 4 |
存在唯一的θ∈[0,2π),使f(θ)≤0,
则:sinθ=
| k-4 |
| 2 |
-1≤
| k-4 |
| 2 |
解得:2≤k≤6;
联立:-4≤k≤4,
∴2≤k≤4,
此时θ=arcsin
| k-4 |
| 2 |
故答案为:(1)θ=
| 7π |
| 6 |
| 11π |
| 6 |
| 7 |
| 4 |
| π |
| 2 |
(2)-4≤k≤4;
(3)2≤k≤4,θ=arcsin
| k-4 |
| 2 |
点评:本题考查的知识点:三角函数的恒等变换,二次函数一般式和顶点式的互化,二次函数的值域,函数的恒成立问题,及相关的运算问题.

练习册系列答案
相关题目
已知二次函数y=-x2+1,则它与x轴所围图形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
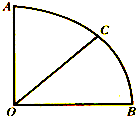 如图,在圆心角为90°的扇形中以圆心.为起点作射线OC,则使得∠AOC与∠BOC都不大于60°的概率是( )
如图,在圆心角为90°的扇形中以圆心.为起点作射线OC,则使得∠AOC与∠BOC都不大于60°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知a,b,c都是正实数,且满足log9(9a+b)=log3
,则使4a+b≥c恒成立的c的取值范围是( )
| ab |
A、[
| ||
| B、(0,22) | ||
| C、[2,23) | ||
| D、(0,25] |