题目内容
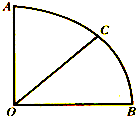如图，在圆心角为90°的扇形中以圆心．为起点作射线OC，则使得∠AOC与∠BOC都不大于60°的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：应用题,概率与统计
分析：本题利用几何概型求解．只须求出满足：使使得∠AOC与∠BOC都不大于60°，再将求得的角度值与整个扇形的角度求比值即得．
解答：
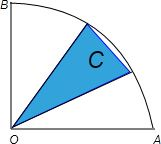解：选角度作为几何概型的测度，
则使得∠AOC与∠BOC都不大于60°的概率是：P=
=
，
故选B．
解：选角度作为几何概型的测度，则使得∠AOC与∠BOC都不大于60°的概率是：P=
| 30 |
| 90 |
| 1 |
| 3 |
故选B．
点评：本小题主要考查几何概型、几何概型中测度的选择等基础知识，考查运算求解能力、化归与转化思想．属于基础题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
对某班级50名学生学习数学与学习物理的成绩进行调查，得到如表所示：
由K2=
，解得K2=
≈11.5
参照附表，得到的正确结论是（ ）
| 数学成绩较好 | 数学成绩一般 | 合计 | |
| 物理成绩较好 | 18 | 7 | 25 |
| 物理成绩一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 50×(18×19-6×7)2 |
| 25×25×24×26 |
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩有关” |
| B、在犯错误的概率不超过0.1%的前提下，认为“数学成绩与物理成绩无关” |
| C、有100%的把握认为“数学成绩与物理成绩有关” |
| D、有99%以上的把握认为“数学成绩与物理成绩无关” |
下面给出四个命题的表述：
①直线（1+m）x+4y-3+m=0（m∈R）恒过定点（-1，1）；
②已知直线l：x-y+4=0与圆C：（x-1）2+（y-1）2=2，则C上各点到l的距离的最大值为3
；
③已知M={(x，y)|y=
}，N={（x，y）|y=x+b}，若M∩N≠Φ，
则b∈[-
，
]；其中表述正确的是（ ）
①直线（1+m）x+4y-3+m=0（m∈R）恒过定点（-1，1）；
②已知直线l：x-y+4=0与圆C：（x-1）2+（y-1）2=2，则C上各点到l的距离的最大值为3
| 2 |
③已知M={(x，y)|y=
| 1-x2 |
则b∈[-
| 2 |
| 2 |
| A、①② | B、①②③ | C、①③ | D、②③ |
在△ABC中，若sinA：sinB：sinC=3：5：7，则这个三角形的最大内角为（ ）
| A、120° | B、150° |
| C、90° | D、60° |