题目内容
已知椭圆
+y2=1,若此椭圆上存在不同的两点A、B关于直线y=2x+m对称,则实数m的取值范围是( )
| x2 |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0).根据此椭圆上存在不同的两点A、B关于直线y=2x+m对称,
可设直线AB的方程可设为y=-
x+t.与椭圆方程联立可得△>0,及其根与系数的关系,利用中点坐标公式可得
M(t,
t).代入直线y=2x+m,解得t=-
.代入△>0即可解出.
可设直线AB的方程可设为y=-
| 1 |
| 2 |
M(t,
| 1 |
| 2 |
| 2m |
| 3 |
解答:
解:设A(x1,y1),B(x2,y2),线段AB的中点M(x0,y0).
∵此椭圆上存在不同的两点A、B关于直线y=2x+m对称,
∴直线AB的方程可设为y=-
x+t.
联立
,化为x2-2tx+2t2-2=0.
△=4t2-4(2t2-2)>0,解得t2<2(*).
∴x1+x2=2t,
∴x0=t,y0=-
t+t=
t.
∴M(t,
t).
代入直线y=2x+m可得:
t=2t+m,解得t=-
.
代入(*)可得:(-
)2<2,解得-
<m<
.
∴m的取值范围是-
<m<
.
故选:B.
∵此椭圆上存在不同的两点A、B关于直线y=2x+m对称,
∴直线AB的方程可设为y=-
| 1 |
| 2 |
联立
|
△=4t2-4(2t2-2)>0,解得t2<2(*).
∴x1+x2=2t,
∴x0=t,y0=-
| 1 |
| 2 |
| 1 |
| 2 |
∴M(t,
| 1 |
| 2 |
代入直线y=2x+m可得:
| 1 |
| 2 |
| 2m |
| 3 |
代入(*)可得:(-
| 2m |
| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
∴m的取值范围是-
3
| ||
| 2 |
3
| ||
| 2 |
故选:B.
点评:本题考查了直线与椭圆相交问题转化为方程联立得到根与系数的关系、△>0、轴对称问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知a=(log32)2,b=log322,c=log3(log32),则a,b,c的大小关系是( )
| A、a>b>c |
| B、b>a>c |
| C、b>c>a |
| D、b>a>c |
已知向量
、
满足|
|=2,|
|=3,|
-
|=
,则
•
=( )
| m |
| n |
| m |
| n |
| m |
| n |
| 17 |
| m |
| n |
A、-
| ||
| B、-1 | ||
| C、-2 | ||
| D、-4 |
在等比数列{an}中,a1=1,公比|q|≠1.若am=a1a2a3a4a5,则m=( )
| A、9 | B、10 | C、11 | D、12 |
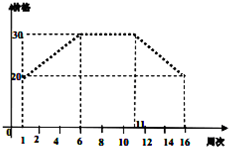 在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.