题目内容
已知命题“函数f(x)=log2(x2+ax+1)定义域为R”是假命题,则实数a的取值范围是 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据对数函数的图象和性质,转化为一元二次函数问题即可得到结论.
解答:
解:若函数f(x)=log2(x2+ax+1)定义域为R,为假命题,
则x2+ax+1>0恒成立为假命题,
即对应的判别式△=a2-4≥0,解得a≤-2或a≥2,
故答案为:a≤-2或a≥2
则x2+ax+1>0恒成立为假命题,
即对应的判别式△=a2-4≥0,解得a≤-2或a≥2,
故答案为:a≤-2或a≥2
点评:本题主要考查,命题的真假应用,结合对数函数和二次函数的性质是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将自然数1,2,3,…,n,…按第k组含k个数的规则分组:(1),(2,3),(4,5,6),…那么2012所在的组是( )
| A、第64组 | B、第63组 |
| C、第62组 | D、第61组 |
在等差数列{an}中,2a3+a9=3,则数列{an}的前9项和等于( )
| A、9 | B、6 | C、3 | D、12 |
已知椭圆
+y2=1,若此椭圆上存在不同的两点A、B关于直线y=2x+m对称,则实数m的取值范围是( )
| x2 |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
已知数列{an}满足a1=
,且对任意的正整数m,n,都有am+n=am•an,则{an}前n项和Sn等于( )
| 2 |
| 3 |
A、2-(
| ||
B、2-(
| ||
C、2-
| ||
D、2-
|
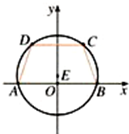 如图,等腰梯形ABCD的底边AB和CD长分别为6和
如图,等腰梯形ABCD的底边AB和CD长分别为6和