题目内容
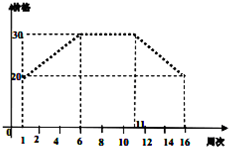 在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.
在某服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为20元/件(第一周价格),并且每周价格上涨,如图所示,从第6周开始到第11轴保持30元/件的价格平稳销售;从第12周开始,当季节即将过去时,每周下跌,直到第16周周末,该服装不再销售.(1)求销售价y(元/件)与周次x之间的函数关系式;
(2)若这种时装每件进价Z与周次x次之间的关系为Z=-0.125(x-8)2+12.(1≤x≤16,且x为整数),试问该服装第几周出售时每件销售利润最大?最大利润为多少?
考点:函数最值的应用
专题:应用题
分析:(1)根据函数图象求出函数解析式即可;
(2)由于y与x之间的函数关系式为分段函数,则w与x之间的函数关系式亦为分段函数,分情况解答.
(2)由于y与x之间的函数关系式为分段函数,则w与x之间的函数关系式亦为分段函数,分情况解答.
解答:
解:(1)依题意得,可建立的函数关系式为:
∴y=
;
即y=
;
(2)设利润为W,则W=售价-进价
故W=
,
化简得W=
,
①当W=
x2+14时,∵当x≥0,函数W随着x增大而增大,∵1≤x<6
∴当x=5时,W有最大值,最大值=17.125
②当W=
x2-2x+26时,∵W=
(x-8)2+18,当x≥8时,函数W随x增大而增大,
∴在x=11时,函数有最大值为19
;
③当W=
x2-4x+48时,∵W=
(x-16)2+16,
∵12≤x≤16,当x≤16时,函数W随x增大而减小,
∴在x=12时,函数有最大值为18
综上所述,当x=11时,函数有最大值为19
.
∴y=
|
即y=
|
(2)设利润为W,则W=售价-进价
故W=
|
化简得W=
|
①当W=
| 1 |
| 8 |
∴当x=5时,W有最大值,最大值=17.125
②当W=
| 1 |
| 8 |
| 1 |
| 8 |
∴在x=11时,函数有最大值为19
| 1 |
| 8 |
③当W=
| 1 |
| 8 |
| 1 |
| 8 |
∵12≤x≤16,当x≤16时,函数W随x增大而减小,
∴在x=12时,函数有最大值为18
综上所述,当x=11时,函数有最大值为19
| 1 |
| 8 |
点评:本题考查的是二次函数的运用,由于计算量大,考生在做这些题的时候要耐心细心.难度中上.此题是分段函数,题目所涉及的内容在求解过程中,要注意分段函数问题先分段解决,最后再整理、归纳得出最终结论,另外还要考虑结果是否满足各段的要求,这是解此类综合应用题目的特点.

练习册系列答案
相关题目
已知椭圆
+y2=1,若此椭圆上存在不同的两点A、B关于直线y=2x+m对称,则实数m的取值范围是( )
| x2 |
| 4 |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
执行如图所示的程序框图,如果输入的x,y∈R,那么输出的S的最大值为( )

| A、0 | B、1 | C、2 | D、3 |
若
=
,则sinα+cosα的值为( )
| cos(2α+π) | ||
sin(α-
|
| ||
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
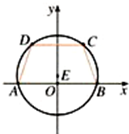 如图,等腰梯形ABCD的底边AB和CD长分别为6和
如图,等腰梯形ABCD的底边AB和CD长分别为6和