题目内容
20.抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 确定抛物线的焦点位置,进而可确定抛物线的焦点坐标;求出双曲线渐近线方程,利用点到直线的距离公式可得结论.
解答 解:抛物线y2=16x的焦点F的坐标为(4,0);双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的一条渐近线方程为$\sqrt{3}$x-y=0,
∴抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的一条渐近线的距离为$\frac{4\sqrt{3}}{\sqrt{3+1}}$=2$\sqrt{3}$,
故选:D.
点评 本题考查双曲线、抛物线的标准方程,以及双曲线、抛物线的简单性质,考查点到直线的距离公式的应用,求出焦点坐标和一条渐近线方程,是解题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知奇函数f(x)满足$f(x+\frac{3}{2})=-f(x)$,且当x∈(0,2)时,f(x)=2x,则f(5)=( )
| A. | 32 | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
15.若x∈R,则(1-|x|)(1+x)>0的解集是( )
| A. | {x|0≤x<1} | B. | {x|x<0且x≠-1} | C. | {x|-1<x<1} | D. | {x|x<1且x≠-1} |
12.为了得到函数$y=2sin({3x+\frac{π}{6}})$的图象,只需把y=2sinx的图象上所有的点( )
| A. | 向右平移$\frac{π}{6}$,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| B. | 向左平移$\frac{π}{6}$,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| C. | 向右平移$\frac{π}{6}$,再把所得各点的横坐标伸长到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| D. | 向左平移$\frac{π}{6}$,再把所得各点的横坐标伸长到原来的$\frac{1}{3}$倍(纵坐标不变) |
10.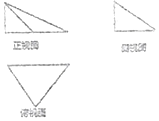 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )| A. | 36π | B. | 9π | C. | $\frac{9}{2}π$ | D. | $\frac{27}{5}π$ |
 如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.
如图,四棱锥P-ABCD中,AD∥BC,$AB=BC=\frac{1}{2}AD$,E,F,H分别为线段AD,PC,CD的中点,AC与BE交于O点,G是线段OF上一点.