题目内容
10.已知奇函数f(x)满足$f(x+\frac{3}{2})=-f(x)$,且当x∈(0,2)时,f(x)=2x,则f(5)=( )| A. | 32 | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
分析 由已知得f(x+3)=-f(x+$\frac{3}{2}$)=f(x),从而f(5)=f(-1)=-f(1),再由当x∈(0,2)时,f(x)=2x,能求出结果.
解答 解:∵奇函数f(x)满足$f(x+\frac{3}{2})=-f(x)$,
∴f(x+3)=-f(x+$\frac{3}{2}$)=f(x),
∵当x∈(0,2)时,f(x)=2x,
∴f(5)=f(-1)=-f(1)=-2.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
19.曲线f(x)=$\frac{1}{3}$x3-2在点(-1,f(-1))处切线的斜率为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
5.执行如图所示的程序框图,则输出S=( )
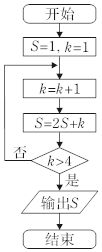

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
15.已知函f(x)数的导数f′(x)=3x2-3ax,f(0)=b,a,b为实数,1<a<2.若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,则a-b的值为$\frac{1}{3}$.
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
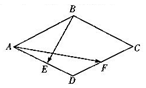

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
20.抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |