题目内容
11.已知△ABC是边长为2的等边三角形,则$\overrightarrow{AB}$•$\overrightarrow{BC}$=-2.分析 由题意可知$\overrightarrow{AB}、\overrightarrow{BC}$的夹角为$\frac{2π}{3}$,然后直接代入数量积公式求解.
解答 解:如图,
$\overrightarrow{AB}$•$\overrightarrow{BC}$=$|\overrightarrow{AB}||\overrightarrow{BC}|cos\frac{2π}{3}=2×2×(-\frac{1}{2})=-2$.
故答案为:-2.
点评 本题考查平面向量的数量积运算,是基础的计算题.

练习册系列答案
相关题目
19.菱形ABCD中,E,F分别是AD,CD中点,若∠BAD=60°,AB=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$=( )
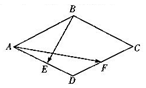

| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
16.0<a<1是函数f(x)=2ax2+1取值恒为正的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
20.抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
1.若集合M={x|(x-1)(x-4)=0},N={x|(x+1)(x-3)<0},则M∩N=( )
| A. | ∅ | B. | {1} | C. | {4} | D. | {1,4} |