题目内容
15.若x∈R,则(1-|x|)(1+x)>0的解集是( )| A. | {x|0≤x<1} | B. | {x|x<0且x≠-1} | C. | {x|-1<x<1} | D. | {x|x<1且x≠-1} |
分析 讨论x>0,x=0,x<0,去掉绝对值,运用二次不等式的解法,即可得到所求解集.
解答 解:当x>0时,(1-|x|)(1+x)>0即为(1-x)(1+x)>0,
解得0<x<1;
当x=0时,1>0显然成立;
当x<0时,(1-|x|)(1+x)>0即为(1+x)(1+x)>0,
解得x<0且x≠-1.
综上可得,解集为{x|x<1且x≠-1},
故选:D.
点评 本题考查不等式的解法,注意运用分类讨论的思想方法,考查运算能力,属于基础题.

练习册系列答案
相关题目
5.执行如图所示的程序框图,则输出S=( )
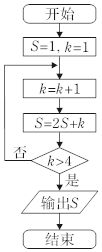

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
6.正方体的棱长为2$\sqrt{3}$,顶点都在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 288π | D. | 144π |
20.抛物线y2=16x的焦点到双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的渐近线的距离是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
5.某租车公司给出的财务报表如下:
有投资者在研究上述报表时,发现租车公司有空驶情况,并给出空驶率的计算公式为$T=\frac{t-ak}{ak}•100%$.
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
 | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
(1)分别计算2014,2015年该公司的空驶率的值(精确到0.01%);
(2)2016年该公司加强了流程管理,利用租车软件,降低了空驶率并提高了平均每单里程,核算截止到11月30日,空驶率在2015年的基础上降低了20个百分点,问2016年前11个月的平均每单油费和平均每单里程分别为多少?(分别精确到0.01元和0.01公里)
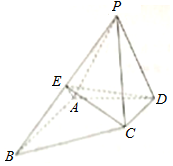 如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
如图,四棱锥P-ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点