题目内容
已知在正整数数列{an}中,其前n项的和为Sn且满足Sn=
(an+2)2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
,求数列{bn}的前n项的和Tn.
| 1 |
| 8 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=
| 1 |
| anan+1 |
考点:数列的求和,数列递推式
专题:计算题,等差数列与等比数列
分析:(Ⅰ)令n=1,易求a1=2,当n≥2时,an=Sn-Sn-1=
(an+2)2-
(an-1+2)2=
(an+an-1+4)(an-an-1),化简可得an-an-1=4,从而判断{an}是等差数列,由等差数列的通项公式可求an;
(Ⅱ)先求出bn=
(
-
),利用裂相消法可求得Tn.
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
(Ⅱ)先求出bn=
| 1 |
| 8 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)当n=1时,S1=a1=
(a1+2)2,解得a1=2;
当n≥2时,an=Sn-Sn-1=
(an+2)2-
(an-1+2)2=
(an+an-1+4)(an-an-1),
∴
-
-4(an+an-1)=0,即(an+an-1)(an-an-1-4)=0,
又数列{an}的各项均为正整数,∴an>0,∴an-an-1=4,
故数列{an}是首项为2,公差为4的等差数列.
∴an=2+4(n-1)=4n-2.
(Ⅱ)bn=
=
=
=
(
-
),
故Tn=b1+b2+…+bn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.
| 1 |
| 8 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
∴
| a | 2 n |
| a | 2 n-1 |
又数列{an}的各项均为正整数,∴an>0,∴an-an-1=4,
故数列{an}是首项为2,公差为4的等差数列.
∴an=2+4(n-1)=4n-2.
(Ⅱ)bn=
| 1 |
| anan+1 |
| 1 |
| (4n-2)(4n+2) |
| 1 |
| 4(2n-1)(2n+1) |
| 1 |
| 8 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
故Tn=b1+b2+…+bn=
| 1 |
| 8 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 8 |
| 1 |
| 2n+1 |
| n |
| 4(2n+1) |
点评:该题考查由递推式求数列通项、等差数列的通项公式、数列求和,考查学生的推理论证能力,裂项相消法对数列求和是高考考查的重点内容,要熟练掌握.

练习册系列答案
相关题目
将一枚骰子先后掷两次,向上点数之和为x,则x≥7的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=|x2-4|-3x+m恰有两个不同的零点,则实数m的取值范围是( )
A、(-6,6)∪(
| ||
B、(
| ||
C、(-∞,-
| ||
D、(-
|
设直线l经过点P(2,1),且A(0,4)、B(4,8)两点到直线l的距离相等,则直线l的方程是( )
| A、x-y-1=0 |
| B、x-y-1=0或x-y-4=0 |
| C、x+y-3=0 |
| D、x-y-1=0或x=2 |
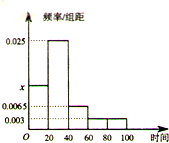 某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).
某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100).