题目内容
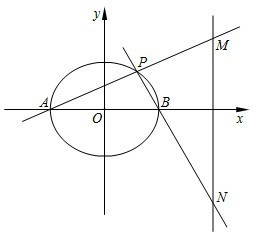已知A，B分别是椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| b2 |
| 4 |
（1）求椭圆C的标准方程；
（2）点P为椭圆C上除长轴端点外的任一点，直线AP，PB与椭圆的右准线分别交于点M，N．
①在x轴上是否存在一个定点E，使得EM⊥EN？若存在，求点E的坐标；若不存在，说明理由；
②已知常数λ＞0，求
| PM |
| PN |
| PA |
| PB |
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）利用直线DA与直线DB的斜率之积为-
，可得b2=
，由点D(1，
)在椭圆C上，则有：
+
=1，联立求出a，b，即可求椭圆C的标准方程；
（2）①假设存在一个定点E（m，0），使得EM⊥EN．确定M，N的坐标，若EM⊥EN，则
•
=0，结合点P在椭圆C上，即可求点E的坐标；
②利用向量的数量积公式，可得
•
+λ
•
=
，设函数f(x0)=
，定义域为（-2，2），确定函数的单调性，即可求得结论．
| b2 |
| 4 |
| 9 |
| a2-1 |
| 3 |
| 2 |
| 1 |
| a2 |
(
| ||
| b2 |
（2）①假设存在一个定点E（m，0），使得EM⊥EN．确定M，N的坐标，若EM⊥EN，则
| EM |
| EN |
②利用向量的数量积公式，可得
| PM |
| PN |
| PA |
| PB |
| (1+λ)x02-8x0+16-4λ |
| 4 |
| (1+λ)x02-8x0+16-4λ |
| 4 |
解答：
解：（1）由题意得，A（-a，0），B（a，0），
∵直线DA与直线DB的斜率之积为-
，
∴kDA•kDB=
•
=-
，∴b2=
，
由点D(1，
)在椭圆C上，则有：
+
=1，…（2分）
由以上两式可解得a2=4，b2=3．
∴椭圆方程为
+
=1． …（4分）
（2）①椭圆右准线的方程为x=4． …（5分）
假设存在一个定点E（m，0），使得EM⊥EN．
设点P（x0，y0）（x0≠±2），直线AP的方程为y=
(x+2)，
令x=4，y=
，∴点M坐标为(4，
)．
直线BP的方程为y=
(x-2)，令x=4，y=
，
∴点N坐标为(4，
)． …（7分）
若EM⊥EN，则
•
=0，
∵
=(4-m，
)，
=(4-m，
)，
∴
•
=(4-m)2+
•
=(4-m)2+
=0． …（9分）
∵点P在椭圆C上，∴
+
=1，∴y02=3(1-
)，代入上式，得（4-m）2=9，
∴m=1或m=7，∴点E的坐标为（1，0）或（7，0）． …（11分）
②∵
=(4-x0，
)，
=(4-x0，
)，
∴
•
=(4-x0)2+
=
．
∵
=(-2-x0，-y0)，
=(2-x0，-y0)，
∴
•
=x02-4+y02=
．
∴
•
+λ
•
=
． …（13分）
设函数f(x0)=
，定义域为（-2，2），
当
≥2时，即0＜λ≤1时，f（x0）在（-2，2）上单调递减，f（x0）的取值范围为（1，9），
当
＜2时，即λ＞1时，f（x0）在(-2，
)上单调递减，在(
，2)上单调递增，f（x0）的取值范围为[
，9)．
综上，当0＜λ≤1时，
•
+λ
•
的取值范围为（1，9），
当λ＞1时，
•
+λ
•
的取值范围为[
，9)． …（16分）
∵直线DA与直线DB的斜率之积为-
| b2 |
| 4 |
∴kDA•kDB=
| ||
| 1+a |
| ||
| 1-a |
| b2 |
| 4 |
| 9 |
| a2-1 |
由点D(1，
| 3 |
| 2 |
| 1 |
| a2 |
(
| ||
| b2 |
由以上两式可解得a2=4，b2=3．
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）①椭圆右准线的方程为x=4． …（5分）
假设存在一个定点E（m，0），使得EM⊥EN．
设点P（x0，y0）（x0≠±2），直线AP的方程为y=
| y0 |
| x0+2 |
令x=4，y=
| 6y0 |
| x0+2 |
| 6y0 |
| x0+2 |
直线BP的方程为y=
| y0 |
| x0-2 |
| 2y0 |
| x0-2 |
∴点N坐标为(4，
| 2y0 |
| x0-2 |
若EM⊥EN，则
| EM |
| EN |
∵
| EM |
| 6y0 |
| x0+2 |
| EN |
| 2y0 |
| x0-2 |
∴
| EM |
| EN |
| 6y0 |
| x0+2 |
| 2y0 |
| x0-2 |
| 12y02 |
| x02-4 |
∵点P在椭圆C上，∴
| x02 |
| 4 |
| y02 |
| 3 |
| x02 |
| 4 |
∴m=1或m=7，∴点E的坐标为（1，0）或（7，0）． …（11分）
②∵
| PM |
| y0(4-x0) |
| x0+2 |
| PN |
| y0(4-x0) |
| x0-2 |
∴
| PM |
| PN |
| y02(4-x 0)2 |
| x02-4 |
| (4-x 0)2 |
| 4 |
∵
| PA |
| PB |
∴
| PA |
| PB |
| x 02-4 |
| 4 |
∴
| PM |
| PN |
| PA |
| PB |
| (1+λ)x02-8x0+16-4λ |
| 4 |
设函数f(x0)=
| (1+λ)x02-8x0+16-4λ |
| 4 |
当
| 4 |
| 1+λ |
当
| 4 |
| 1+λ |
| 4 |
| 1+λ |
| 4 |
| 1+λ |
| -λ2+3λ |
| 1+λ |
综上，当0＜λ≤1时，
| PM |
| PN |
| PA |
| PB |
当λ＞1时，
| PM |
| PN |
| PA |
| PB |
| -λ2+3λ |
| 1+λ |
点评：本题考查椭圆的方程，考查向量知识的运用，考查函数思想，考查学生分析解决问题的能力，有难度．
练习册系列答案
相关题目
如果执行如图的框图，输入N趋向于+∞，则输出的数S趋向（ ）
| A、1 | ||
B、
| ||
| C、+∞ | ||
D、
|
已知α为锐角，且tan（π-α）+3=0，则sinα的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
