题目内容
已知函数f(x)=ax-2-2(a>0且a≠1)的图象恒过定点A(m,n),则不等式组
所表示的平面区域的面积是 .
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据指数函数的性质求出定点A,然后作出不等式组对应的平面区域,即可求出面积.
解答:
解:根据指数函数的性质可知f(x)=ax-2-2(a>0且a≠1)的图象恒过定点A(2,-1),
即m=2,n=-1,
∴不等式组为
,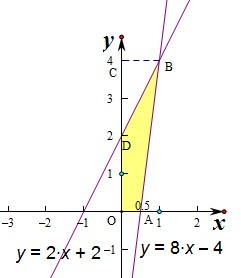
不等式组对应的平面区域为四边形OABD,
则A(
,0),B(1,4),C(0,4),D(0,2),
∴四边形OABD的面积为
-
×1×(4-2)=3-1=2,
故答案为:2
即m=2,n=-1,
∴不等式组为
|
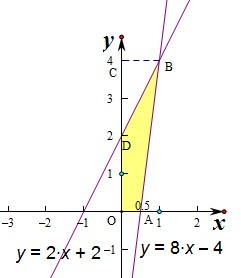
不等式组对应的平面区域为四边形OABD,
则A(
| 1 |
| 2 |
∴四边形OABD的面积为
(1+
| ||
| 2 |
| 1 |
| 2 |
故答案为:2
点评:本题主要考查二元一次不等式组表示平面区域的内容,根据指数函数的性质求出m,n的值是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.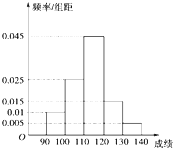 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.