题目内容
 如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.
如图,AB是的⊙O直径,CB与⊙O相切于B,E为线段CB上一点,连接AC、AE分别交⊙O于D、G两点,连接DG交CB于点F.(Ⅰ)求证:C、D、G、E四点共圆.
(Ⅱ)若F为EB的三等分点且靠近E,EG=1,GA=3,求线段CE的长.
考点:与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)连接BD,由题设条件结合圆的性质能求出∠C=∠AGD,从而得到∠C+∠DGE=180°,由此能证明C,E,G,D四点共圆.
(Ⅱ)由切割线定理推导出EB=2,由此能求出CE的长.
(Ⅱ)由切割线定理推导出EB=2,由此能求出CE的长.
解答:
(Ⅰ)证明:连接BD,则∠AGD=∠ABD,
∵∠ABD+∠DAB=90°,∠C+∠CAB=90°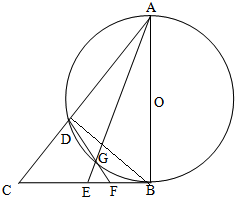
∴∠C=∠AGD,
∴∠C+∠DGE=180°,
∴C,E,G,D四点共圆.…..(5分)
(Ⅱ)解:∵EG•EA=EB2,EG=1,GA=3,
∴EB=2,
又∵F为EB的三等分点且靠近E,
∴EF=
,FB=
,
又∵FG•FD=FE•FC=FB2,
∴FC=
,CE=2.….(10分)
∵∠ABD+∠DAB=90°,∠C+∠CAB=90°

∴∠C=∠AGD,
∴∠C+∠DGE=180°,
∴C,E,G,D四点共圆.…..(5分)
(Ⅱ)解:∵EG•EA=EB2,EG=1,GA=3,
∴EB=2,
又∵F为EB的三等分点且靠近E,
∴EF=
| 2 |
| 3 |
| 4 |
| 3 |
又∵FG•FD=FE•FC=FB2,
∴FC=
| 8 |
| 3 |
点评:本题考查四点共圆的证明,考查线段长的求法,是中档题,解题时要注意圆的性质的灵活运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
复数z=
在复平面上对应的点的坐标为( )
| 1-i |
| 2+i |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
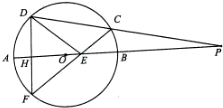 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.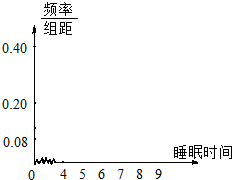 某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.