题目内容
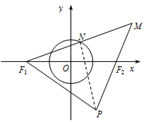如图，已知定点F1（-2，0），F2（2，0），动点N满足|| ON |
| F1M |
| 2NM |
| MP |
| MF2 |
| F1M |
| PN |
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定||PF1|-|PF2||=||PM|-|PF2||=|MF2|=2＜|F1F2|，由双曲线的定义可知：点P的轨迹是以F1，F2为焦点的双曲线，从而可得点P的轨迹方程．
解答：
解：连接ON，则
∵
=
，
∴点N是MF1中点，
∴|MF2|=2|NO|=2
∵
•
=0，
∴F1M⊥PN，
∴|PM|=|PF1|
∴||PF1|-|PF2||=||PM|-|PF2||=|MF2|=2＜|F1F2|
由双曲线的定义可知：点P的轨迹是以F1，F2为焦点的双曲线．
∴点P的轨迹方程是x2-
=1．
∵
| F1M |
| 2NM |
∴点N是MF1中点，
∴|MF2|=2|NO|=2
∵
| F1M |
| PN |
∴F1M⊥PN，
∴|PM|=|PF1|
∴||PF1|-|PF2||=||PM|-|PF2||=|MF2|=2＜|F1F2|
由双曲线的定义可知：点P的轨迹是以F1，F2为焦点的双曲线．
∴点P的轨迹方程是x2-
| y2 |
| 3 |
点评：本题考查轨迹方程，考查向量知识的应用，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知l，m，n是三条不同的直线，α，β是不同的平面，则下列条件中能推出α⊥β的是（ ）
| A、l?α，m?β，且l⊥m |
| B、l?α，m?β，n?β，且l⊥m，l⊥n |
| C、m?α，n?β，m∥n，且l⊥m |
| D、l?α，l∥m，且m⊥β |