题目内容
已知二次函数y=f(x)经过点(1,20),其导函数f′(x)=4x-22.数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)均在函数y=f(x)的图象上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{|an|}前n项和为Tn,求Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{|an|}前n项和为Tn,求Tn.
考点:数列与函数的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用导数的性质,求出f(x)=2x2-22x+40,从而得到Sn=2n2-22n+40,由此能求出数列{an}通项公式.
(Ⅱ)由(Ⅰ)得到|an|=
,由此能求出数列{|an|}前n项和Tn.
(Ⅱ)由(Ⅰ)得到|an|=
|
解答:
解:(Ⅰ)∵f′(x)=4x-22,
∴f(x)=2x2-22x+c,
∵y=f(x)经过点(1,20),∴c=40,∴f(x)=2x2-22x+40.
∵数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)均在函数y=f(x)的图象上,
∴Sn=2n2-22n+40,
当n≥2时,an=Sn-Sn-1=2n2-22n+40-2(n-1)2+22(n-1)-40
=4n-24,…(3分)
当n=1时,a1=20
所以数列通项an=
.…(3分)
(Ⅱ)∵an=
,
∴|an|=
,
∴当n≤6时,Tn=
=n(22-2n)…(3分)
当n≥7时,Tn=T6+
=60+(2n-10)(n-6)=2n2-22n+120.
∴Tn=
.(3分)
∴f(x)=2x2-22x+c,
∵y=f(x)经过点(1,20),∴c=40,∴f(x)=2x2-22x+40.
∵数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)均在函数y=f(x)的图象上,
∴Sn=2n2-22n+40,
当n≥2时,an=Sn-Sn-1=2n2-22n+40-2(n-1)2+22(n-1)-40
=4n-24,…(3分)
当n=1时,a1=20
所以数列通项an=
|
(Ⅱ)∵an=
|
∴|an|=
|
∴当n≤6时,Tn=
| (20+24-4n)n |
| 2 |
当n≥7时,Tn=T6+
| (4+4n-24)(n-6) |
| 2 |
=60+(2n-10)(n-6)=2n2-22n+120.
∴Tn=
|
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意导数性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x|x2-5x-6<0},B={x||x|<2},则A∩(∁RB)=( )
| A、(-1,2) |
| B、[-1,2) |
| C、(2,6) |
| D、[2,6) |
若函数y=cosωx(ω>0)的图象向右平移
个单位后与函数y=sinωx的图象重合,则ω的值可能是( )
| π |
| 6 |
A、
| ||
| B、1 | ||
| C、3 | ||
| D、4 |
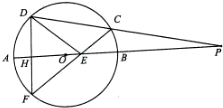 已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.
已知:如图,P是⊙O的直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF与直线AB垂直,H为垂足,CF与AB交于点E.