题目内容
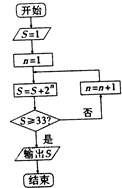
如图是一个算法流程图，则输出S的值是（ ）
| A、31 | B、32 | C、63 | D、64 |
考点：程序框图
专题：算法和程序框图
分析：先弄清流程图所表示的含义，该流程图表示求S=1+21+22+23+…+2n＞33的S的最小的值，然后根据等比数列的求和公式解之即可求出所求．
解答：
解：由程序框图可得，表示求S=1+21+22+23+…+2n＞33的最小的S的值，
当n=4时，S=1+21+22+23+24=31＜33，
当n=5时，S=1+21+22+23+24+25=63＞33，
∴退出循环，此时输出的S=63，
故选C．
当n=4时，S=1+21+22+23+24=31＜33，
当n=5时，S=1+21+22+23+24+25=63＞33，
∴退出循环，此时输出的S=63，
故选C．
点评：本题主要考查了等比数列的求和，以及流程图的含义和循环结构，弄清循环的次数是解题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
已知点P（-2，1）是角θ终边上一点，则sinθ=（ ）
| A、2 | ||||
B、-
| ||||
C、-
| ||||
D、
|
若角α的终边过点（-1，2），则cos2α的值为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数y=-x2+1，-1≤x＜2的值域是（ ）
| A、（-3，0] |
| B、[0，1] |
| C、（-3，1] |
| D、[1，5） |
在△ABC中，AC=6，BC=7，cosA=
，O是△ABC的内心，在△ABC内随机任取一点P，则取到满足条件
=x
+y
（0≤x≤1且0≤y≤1）时的点P的概率为（ ）
| 1 |
| 5 |
| OP |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={0，a}，B={x∈Z||x|＜2 }，则“a=1”是“A⊆B”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
已知集合A={2a}，B={a，b），若A∩B={
}，则A∪B为（ ）
| 1 |
| 2 |
A、{
| ||
B、{-1，
| ||
C、{
| ||
D、{-1，
|
已知命题p：若非零实数a，b，则
＜
；命题q：对任意实数x∈（0，+∞），log
（x+1）＜0，则下列命题为真命题的是（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| 2 |
| A、p且q | B、p或￢q |
| C、￢p且q | D、p且￢q |
