题目内容
函数y=-x2+1，-1≤x＜2的值域是（ ）
| A、（-3，0] |
| B、[0，1] |
| C、（-3，1] |
| D、[1，5） |
考点：二次函数的性质
专题：函数的性质及应用
分析：由x的取值范围逐步求出-x2+1的取值范围，问题得解．
解答：
解：∵-1≤x＜2，
∴0≤x2＜4，
∴-4＜-x2≤0，
∴-3＜-x2+1≤1，
故选：C．
∴0≤x2＜4，
∴-4＜-x2≤0，
∴-3＜-x2+1≤1，
故选：C．
点评：本题考察了求函数的值域问题，可通过计算逐步推出，也可画出草图一目了然，本题是一道基础题．
练习册系列答案
相关题目
四边形OABC中，
=
，若
=
，
=
，则
=（ ）
| CB |
| 1 |
| 2 |
| OA |
| OA |
| a |
| OC |
| b |
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知等比数列{an}的公比q＞0，且a5a7=4a42，a2=1，则a1=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知命题p：随机变量x～N（2，σ2），且p（x＞3）=0.3010，则p（1≤x＜2）=0.1990，命题q：若向量
，
满足|
|=1，|
|=3，
与
夹角为
，则|
+
|=
．下面结论正确的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| 7 |
| A、（￢p）∨q是真命题 |
| B、p∨q是假命题 |
| C、p∧q是真命题 |
| D、p∧（￢q）是真命题 |
如图是一个算法流程图，则输出S的值是（ ）
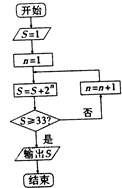
| A、31 | B、32 | C、63 | D、64 |
二次函数y=f（x）的图象的一部分如图所示