题目内容
已知集合A={2a},B={a,b),若A∩B={
},则A∪B为( )
| 1 |
| 2 |
A、{
| ||
B、{-1,
| ||
C、{
| ||
D、{-1,
|
考点:并集及其运算
专题:集合
分析:由A与B,以及两集合的交集确定出a与b的值,进而确定出A与B,求出两集合的并集即可.
解答:
解:∵A={2a},B={a,b),且A∩B={
},
∴2a=
,a=
或b=
,
解得:a=-1,b=
,
∴A={
},B={-1,
},
则A∩B={-1,
}.
故选:B.
| 1 |
| 2 |
∴2a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:a=-1,b=
| 1 |
| 2 |
∴A={
| 1 |
| 2 |
| 1 |
| 2 |
则A∩B={-1,
| 1 |
| 2 |
故选:B.
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
已知等比数列{an}的公比q>0,且a5a7=4a42,a2=1,则a1=( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
如图是一个算法流程图,则输出S的值是( )
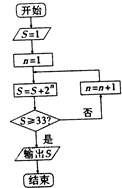

| A、31 | B、32 | C、63 | D、64 |
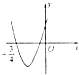 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
给出以下四个命题:
①命题“?x<0,x2-x>0”的否定是“?x≥0,x2-x≤0”
②若实数x、y∈[0,1],则满足y>
的概率是
③若随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,则P(0<ξ<2)=0.3
④若a>b≥2,则b2>3b-a
其中真命题有( )
①命题“?x<0,x2-x>0”的否定是“?x≥0,x2-x≤0”
②若实数x、y∈[0,1],则满足y>
| x |
| 2 |
| 3 |
③若随机变量ξ服从正态分布N(2,ξ2)且P(ξ<4)=0.8,则P(0<ξ<2)=0.3
④若a>b≥2,则b2>3b-a
其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
函数f(x)=ax2-ax+1(a≠0),如果f(-k)<0,则f(k+1)的值是( )
| A、正数 | B、负数 | C、零 | D、无法确定 |