题目内容
在△ABC中,AC=6,BC=7,cosA=
,O是△ABC的内心,在△ABC内随机任取一点P,则取到满足条件
=x
+y
(0≤x≤1且0≤y≤1)时的点P的概率为( )
| 1 |
| 5 |
| OP |
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:根据条件
=x
+y
(0≤x≤1且0≤y≤1),确定P对应的区域,利用几何槪型求出对应的平面区域的面积即可得到结论.
| OP |
| OA |
| OB |
解答:
解:∵
=x
+y
(0≤x≤1且0≤y≤1),
∴动点P的轨迹是以OA,OB为邻边的平行四边形ADBO的内部(含边界),
∵AC=6,BC=7,cosA=
,
BC2=AC2+AB2-2AB×AC×cosA
∴49=36+AB2-2×6×AB×
,
∴5AB2-12AB-65=0,
解得:AB=5,sinA=
=
,
∴S△ABC=
×6×5×
=6
,
设△ABC内切圆半径为r,则
×(5+6+7)r=6
,
∴r=
∴S△AOB=
×AB×r=
×5×
=
,
∴满足条件
=x
+y
(0≤x≤1且0≤y≤1)时的点P的概率P=
=
=
.
故选:B.

| OP |
| OA |
| OB |
∴动点P的轨迹是以OA,OB为邻边的平行四边形ADBO的内部(含边界),
∵AC=6,BC=7,cosA=
| 1 |
| 5 |
BC2=AC2+AB2-2AB×AC×cosA
∴49=36+AB2-2×6×AB×
| 1 |
| 5 |
∴5AB2-12AB-65=0,
解得:AB=5,sinA=
| 1-cos2A |
2
| ||
| 5 |
∴S△ABC=
| 1 |
| 2 |
2
| ||
| 5 |
| 6 |
设△ABC内切圆半径为r,则
| 1 |
| 2 |
| 6 |
∴r=
2
| ||
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
5
| ||
| 3 |
∴满足条件
| OP |
| OA |
| OB |
| S△AOB |
| S△ABC |
| ||||
6
|
| 5 |
| 18 |
故选:B.

点评:本题主要考查几何槪型的概率的计算,利用向量数量积的意义,确定P的轨迹是解决本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若
=a+bi,(a,b∈R),则(a,b)为( )
| 1 |
| 1-i |
A、(
| ||||
B、(-
| ||||
| C、(1,1) | ||||
| D、(1,-1) |
复数
=( )
| 1+3i |
| 1-i |
| A、2+i | B、2-i |
| C、-1+2i | D、-1-2i |
已知等比数列{an}的公比q>0,且a5a7=4a42,a2=1,则a1=( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
设f(x)是周期为4的奇函数,当0≤x≤2时,f(x)=x(2-x),则f(-5)等于( )
| A、1 | B、-1 | C、3 | D、-3 |
如图是一个算法流程图,则输出S的值是( )
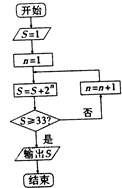

| A、31 | B、32 | C、63 | D、64 |
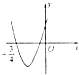 如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )
如图是函数f(x)=x2-ax+b的大致图象,则函数g(x)=log2x+f′(x)的零点所在的区间是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
函数f(x)=ax2-ax+1(a≠0),如果f(-k)<0,则f(k+1)的值是( )
| A、正数 | B、负数 | C、零 | D、无法确定 |