题目内容
设集合A={0，a}，B={x∈Z||x|＜2 }，则“a=1”是“A⊆B”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据集合关系，以及充分条件和必要条件的定义进行判断即可得到结论．
解答：
解：∵B={-1，0，l }，
∴当a=1时，则A={O，l }，
即A⊆B．
若A⊆B，
则a=1或a=-1，
即“a=1”是“A⊆B”的充分不必要条件，
故选：C．
∴当a=1时，则A={O，l }，
即A⊆B．
若A⊆B，
则a=1或a=-1，
即“a=1”是“A⊆B”的充分不必要条件，
故选：C．
点评：本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
一列火车在平直的铁轨上行驶，由于遇到紧急情况，火车以速度v（t）=5-t+
（t的单位：s，v的单位：m/s）紧急刹车至停止，在此期间火车继续行驶的距离是（ ）
| 55 |
| 1+t |
| A、55ln10 |
| B、55ln11 |
| C、12+55ln7 |
| D、12+55ln6 |
四边形OABC中，
=
，若
=
，
=
，则
=（ ）
| CB |
| 1 |
| 2 |
| OA |
| OA |
| a |
| OC |
| b |
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知命题p：随机变量x～N（2，σ2），且p（x＞3）=0.3010，则p（1≤x＜2）=0.1990，命题q：若向量
，
满足|
|=1，|
|=3，
与
夹角为
，则|
+
|=
．下面结论正确的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| 7 |
| A、（￢p）∨q是真命题 |
| B、p∨q是假命题 |
| C、p∧q是真命题 |
| D、p∧（￢q）是真命题 |
如图是一个算法流程图，则输出S的值是（ ）
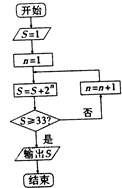
| A、31 | B、32 | C、63 | D、64 |
函数y=2sin（2x+
）的一条对称轴是（ ）
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|