题目内容
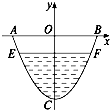 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.(1)求截面图中水面宽度;
(2)如把此水渠改造成横截面是等腰梯形,要求渠深不变,不准往回填土,只准挖土,试求截面梯形的下边长为多大时,才能使所挖的土最少?
考点:抛物线的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先建立直角坐标系,从而可得到A,B,C的坐标,然后设出抛物线的标准形式,将A的坐标代入即可得到抛物线的方程,再结合点E的纵坐标可求得其横坐标,从而可求得EF的宽度.
(2)先设出点M的坐标,根据沿过点M与抛物线相切的切线挖土时挖出的土最少,然后对抛物线方程进行求导,求得点M的切线的斜率,表示出切线方程,然后令y=0、-
,求得对应的x的值,从而表示出截面面积,最后根据基本不等式的性质可求得t的值.
(2)先设出点M的坐标,根据沿过点M与抛物线相切的切线挖土时挖出的土最少,然后对抛物线方程进行求导,求得点M的切线的斜率,表示出切线方程,然后令y=0、-
| 3 |
| 2 |
解答:
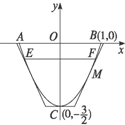 解:(1)建立如图所示坐标系,则抛物线方程为x2=
解:(1)建立如图所示坐标系,则抛物线方程为x2=
(y+
),
当y=-0.5时,x=±
,∴水面宽EF=
m.
(2)如上图,设抛物线一点M(t,
t2-
)(t>0),
因改造水渠中需挖土,而且要求挖出的土最少,所以只能沿过点M与抛物线相切的切线挖土.由y=
x2-
,求导得y′=3x,
∴过点M的切线斜率为3t,切线方程为y-(
t2-
)=3t(x-t).
令y=0,则x1=
,令y=-
,则x2=
,
故截面梯形面积为S=
(2x1+2x2)•
=
(
+t)≥
,
当且仅当t=
时所挖土最少,此时下底宽
m.
 解:(1)建立如图所示坐标系,则抛物线方程为x2=
解:(1)建立如图所示坐标系,则抛物线方程为x2=| 2 |
| 3 |
| 3 |
| 2 |
当y=-0.5时,x=±
| ||
| 3 |
2
| ||
| 3 |
(2)如上图,设抛物线一点M(t,
| 3 |
| 2 |
| 3 |
| 2 |
因改造水渠中需挖土,而且要求挖出的土最少,所以只能沿过点M与抛物线相切的切线挖土.由y=
| 3 |
| 2 |
| 3 |
| 2 |
∴过点M的切线斜率为3t,切线方程为y-(
| 3 |
| 2 |
| 3 |
| 2 |
令y=0,则x1=
| 1+t2 |
| 2t |
| 3 |
| 2 |
| t |
| 2 |
故截面梯形面积为S=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2t |
3
| ||
| 2 |
当且仅当t=
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查抛物线在实际生活中的应用.考查选择恰当参数建立数学式子研究几何图形的解析几何思维;考查根据实际选择数学模型的能力(即数学建模能力).

练习册系列答案
相关题目
已知函数f(x)=ax3+bx2+x(a,b∈R且ab≠0)的图象如图,且|x1|>|x2|,则有( )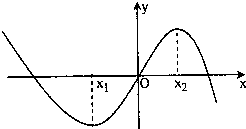

| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |
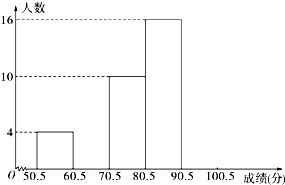 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: