题目内容
设各项均为正数的数列{an}的前n项和为Sn,且Sn满足Sn2-(n2+n-3)Sn-3(n2+n)=0,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有
+
+
+…+
<
.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有
| 1 |
| a1a3 |
| 1 |
| a2a4 |
| 1 |
| a3a5 |
| 1 |
| anan+2 |
| 3 |
| 16 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接在数列递推式中取n=1求得首项;
(2)由原数列递推式求解Sn,再由an=Sn-Sn-1(n≥2)得答案;
(3)利用裂项相消法求和后放缩证明数列不等式.
(2)由原数列递推式求解Sn,再由an=Sn-Sn-1(n≥2)得答案;
(3)利用裂项相消法求和后放缩证明数列不等式.
解答:
解:(1)由Sn2-(n2+n-3)Sn-3(n2+n)=0,n∈N*.
令n=1,得:S12-(-1)S1-3×2=0,即S12+S1-6=0,
∵S1>0,解得a1=S1=2;
(2)由Sn2-(n2+n-3)Sn-3(n2+n)=0,得(Sn+3)[Sn-(n2+n)]=0,
∵an>0,
∴Sn>0,从而Sn+3>0,Sn=n2+n.
当n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
又a1=2,
∴an=2n;
(3)由(2)知,an=2n.
故有
+
+
+…+
=
+
+
+…+
=
[
+
+
+…+
]
=
[
(1-
+
-
+
-
+…+
-
+
-
)]
=
(1+
-
-
)<
(1+
)=
.
令n=1,得:S12-(-1)S1-3×2=0,即S12+S1-6=0,
∵S1>0,解得a1=S1=2;
(2)由Sn2-(n2+n-3)Sn-3(n2+n)=0,得(Sn+3)[Sn-(n2+n)]=0,
∵an>0,
∴Sn>0,从而Sn+3>0,Sn=n2+n.
当n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=2n,
又a1=2,
∴an=2n;
(3)由(2)知,an=2n.
故有
| 1 |
| a1a3 |
| 1 |
| a2a4 |
| 1 |
| a3a5 |
| 1 |
| anan+2 |
| 1 |
| 2×6 |
| 1 |
| 4×8 |
| 1 |
| 6×10 |
| 1 |
| 2n(2n+4) |
=
| 1 |
| 4 |
| 1 |
| 1×3 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| n(n+2) |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 16 |
点评:本题考查了数列递推式,考查了裂项相消法求数列的和,训练了放缩法证明数列不等式,是压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}中,a1=
,an+1=
,则a2014=( )
| 4 |
| 5 |
|
A、
| ||
B、
| ||
C、
| ||
D、
|
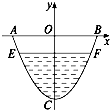 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.