题目内容
已知函数f(x)=ax3+bx2+x(a,b∈R且ab≠0)的图象如图,且|x1|>|x2|,则有( )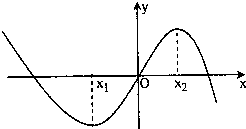

| A、a>0,b>0 |
| B、a<0,b<0 |
| C、a<0,b>0 |
| D、a>0,b<0 |
考点:函数的图象
专题:函数的性质及应用
分析:由图知二个零点x1,x2.从而得导函数f′(x)=3ax2+2bx+1的图象是开口向下、与x轴交于点(x1,0)、(x2,0)的抛物线,又由图得a<0,从而可以判断a,b,c的符号.
解答:
解:由图象可知:
∴导函数f′(x)=3ax2+2bx+1的图象是开口向下、与x轴交于点(x1,0)、(x2,0)的抛物线
∴a<0,x1+x2=
,
由x1<0,x2>0,且|x1|>|x2|知:x1+x2=
∴b<0
故选B.
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
| f′(x) | - | 0 | + | 0 | - |
∴a<0,x1+x2=
| 2b |
| 3a |
由x1<0,x2>0,且|x1|>|x2|知:x1+x2=
| 2b |
| 3a |
∴b<0
故选B.
点评:本题考查函数的零点,三次函数的图象,以及利用图象解决问题的能力.

练习册系列答案
相关题目
双曲线
-
=1(b>0)的焦距为6,则双曲线的渐近线方程为( )
| x2 |
| 4 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
数列{an}中,a1=2,an+1=an+cn(c是常数),且a1,a2,a3成公比不为1的等比数列,则{an}的通项公式为( )
| A、n2+2n-1 |
| B、n2-2n+1 |
| C、n2+n |
| D、n2-n+2 |
已知x+x-1=3,则x3+x-3=( )
A、8
| ||
B、3
| ||
| C、18 | ||
D、±
|
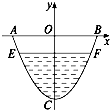 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.