题目内容
已知函数f(x)=|x|(x-a),a为实数.
(1)若g(x)为定义在R的奇函数,当x>0时,g(x)=f(x),求g(x)的解析式;
(2)若关于x的方程f(x)+1=0有3个实数解,求实数a的取值范围;
(3)是否存在实数a,使得f(x)在闭区间[1,2]上的最大值为-4,若存在,求出a的值;若不存在,请说明理由.
(1)若g(x)为定义在R的奇函数,当x>0时,g(x)=f(x),求g(x)的解析式;
(2)若关于x的方程f(x)+1=0有3个实数解,求实数a的取值范围;
(3)是否存在实数a,使得f(x)在闭区间[1,2]上的最大值为-4,若存在,求出a的值;若不存在,请说明理由.
考点:函数奇偶性的性质,函数解析式的求解及常用方法,函数零点的判定定理,根的存在性及根的个数判断
专题:综合题,方程思想,函数的性质及应用
分析:(1)g(x)为定义在R的奇函数,g(-x)=-g(x),运用x>0时,g(x)=f(x)=x(x-a),求得g(x)=
,
(2)函数f(x)=|x|(x-a)=
,分类讨论解决.
(3)转化为二次函数闭区间上的最值讨论.
|
(2)函数f(x)=|x|(x-a)=
|
(3)转化为二次函数闭区间上的最值讨论.
解答:
解:(1)∵g(x)为定义在R的奇函数,∴g(-x)=-g(x),
当x>0时,g(x)=f(x)=x(x-a),
当x=0时,g(0)=0
设x<0时,则-x>0,
∴g(x)=-g(-x)=-[-x(-x-a)]=-x(x+a),(x<0),
即g(x)=
,
(2)函数f(x)=|x|(x-a)=
,
当a≤0时,两段的对称轴为x=
,x=-
,
可判断在(-∞,+∞)单调递增,不可能有3个交点;
当a>0时,若x≥0,对称轴x=
,最小值为-
,
若x<0时,对称轴x=-
,最大值为
,
所以:-
<-1<
,即a>2,a<-2,
综上:实数a的取值范围:(-∞,-2)
(3)当a≤0时判断在(-∞,+∞)单调递增,f(0)=0,在闭区间[1,2]上的最大值为-4,不可能;
当a>0时,若x≥0,对称轴x=
,最小值为-
,
∴
或
解得a=5
所以存在实数a,使得f(x)在闭区间[1,2]上的最大值为-4
当x>0时,g(x)=f(x)=x(x-a),
当x=0时,g(0)=0
设x<0时,则-x>0,
∴g(x)=-g(-x)=-[-x(-x-a)]=-x(x+a),(x<0),
即g(x)=
|
(2)函数f(x)=|x|(x-a)=
|
当a≤0时,两段的对称轴为x=
| a |
| 2 |
| a |
| 2 |
可判断在(-∞,+∞)单调递增,不可能有3个交点;
当a>0时,若x≥0,对称轴x=
| a |
| 2 |
| a2 |
| 4 |
若x<0时,对称轴x=-
| a |
| 2 |
| a2 |
| 4 |
所以:-
| a2 |
| 4 |
| a2 |
| 4 |
综上:实数a的取值范围:(-∞,-2)
(3)当a≤0时判断在(-∞,+∞)单调递增,f(0)=0,在闭区间[1,2]上的最大值为-4,不可能;
当a>0时,若x≥0,对称轴x=
| a |
| 2 |
| a2 |
| 4 |
∴
|
|
解得a=5
所以存在实数a,使得f(x)在闭区间[1,2]上的最大值为-4
点评:本题综合考查了函数的性质,方程思想的运用,不等式的结合,难度较大,做题仔细认真些.

练习册系列答案
相关题目
已知向量
=(1,x),
=(x,3),若
∥
,则|
|=( )
| a |
| b |
| a |
| b |
| a |
| A、1 | ||
B、
| ||
| C、4 | ||
| D、2 |
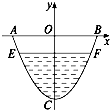 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.