题目内容
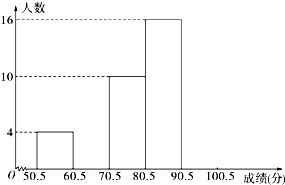 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(2)若成绩在75.5~85.5分的学生为二等奖,请你估计获得二等奖的人数;
(3)用分层抽样的方法从80分以上(不包括80分)的学生中抽取了7人进行试卷分析,再从这7人中选取2人进行经验汇报,求选出的2人至少有1人在[90.5,100.5]的概率.
考点:古典概型及其概率计算公式,分层抽样方法,频率分布直方图
专题:概率与统计
分析:(1)在频率分直方图中,各组的频数=频率×样本容量,小矩形的面积等于这一组的频率,根据频率的和等于1建立等式解之即可;
(2)成绩在75.5~85.5分的学生占成绩在70.5~90.5分的学生的
,进而估算出频率,结合共有900名学生参加了这次竞赛可得答案.;
(3)80.5~90.5与90.5~100.5的人数比为:4:3,所以从80分以上(不包括80分)的学生中抽取了7人中,分数在80.5~90.5的有4人,分数在90.5~100.5的有3人,计算出抽取方法总数和选出的2人至少有1人在[90.5,100.5]抽取方法数,代入古典概型概率计算公式,可得答案.
(2)成绩在75.5~85.5分的学生占成绩在70.5~90.5分的学生的
| 1 |
| 2 |
(3)80.5~90.5与90.5~100.5的人数比为:4:3,所以从80分以上(不包括80分)的学生中抽取了7人中,分数在80.5~90.5的有4人,分数在90.5~100.5的有3人,计算出抽取方法总数和选出的2人至少有1人在[90.5,100.5]抽取方法数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)由已知样本容量为50,故第二组的频数为0.16×50=8,
第三组的频率为
=0.20,
第四组的频数为:50-(4+8+10+16)=12,频率为:
=0.24,
故频率分布表为:
频率分布直方图如下图所示:

(2)成绩在75.5~85.5分的学生占成绩在70.5~90.5分的学生的
,
∵成绩在70.5~90.5分的累加频率为:0.52,
所以成绩在75.5~85.5分,即获得二等奖频率约为0.26,
由于共有900名学生参加了这次竞赛,
所以获得二等奖的学生约为900×0.26=234人,
(3)80.5~90.5与90.5~100.5的人数比为:4:3,
所以从80分以上(不包括80分)的学生中抽取了7人中,分数在80.5~90.5的有4人,分数在90.5~100.5的有3人,
从这7人中选取2人进行经验汇报共有
=21种抽取方法,
其中选出的2人至少有1人在[90.5,100.5]的抽法有:
=15种,
故选出的2人至少有1人在[90.5,100.5]的概率P=
=
第三组的频率为
| 10 |
| 50 |
第四组的频数为:50-(4+8+10+16)=12,频率为:
| 12 |
| 50 |
故频率分布表为:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |

(2)成绩在75.5~85.5分的学生占成绩在70.5~90.5分的学生的
| 1 |
| 2 |
∵成绩在70.5~90.5分的累加频率为:0.52,
所以成绩在75.5~85.5分,即获得二等奖频率约为0.26,
由于共有900名学生参加了这次竞赛,
所以获得二等奖的学生约为900×0.26=234人,
(3)80.5~90.5与90.5~100.5的人数比为:4:3,
所以从80分以上(不包括80分)的学生中抽取了7人中,分数在80.5~90.5的有4人,分数在90.5~100.5的有3人,
从这7人中选取2人进行经验汇报共有
| C | 2 7 |
其中选出的2人至少有1人在[90.5,100.5]的抽法有:
| C | 1 4 |
| C | 1 3 |
| +C | 2 3 |
故选出的2人至少有1人在[90.5,100.5]的概率P=
| 15 |
| 21 |
| 5 |
| 7 |
点评:本题主要考查了频率及频率分布直方图,考查运用统计知识解决简单实际问题的能力,数据处理能力和运用意识.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
函数y=x2cosx的导数为( )
| A、y′=x2cosx-2xsinx |
| B、y′=2xcosx+x2sinx |
| C、y′=2xcosx-x2sinx |
| D、y′=xcosx-x2sinx |
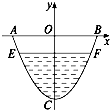 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.