题目内容
某校高三年级有男学生105人,女学生126人,教师42人,用分层抽样的方法从中抽取13人进行问卷调查,设其中某项问题的选择,分别为“同意”、“不同意”两种,且每人都做了一种选择,下面表格中提供了被调查人答卷情况的部分信息.
(1)完成此统计表;
(2)估计高三年级学生“同意”的人数;
(3)从被调查的女学生中选取2人进行访谈,设“同意”的人数为ξ,求Eξ.
| 同意 | 不同意 | 合计 | |
| 教师 | 1 | ||
| 女学生 | 4 | ||
| 男学生 | 2 |
(2)估计高三年级学生“同意”的人数;
(3)从被调查的女学生中选取2人进行访谈,设“同意”的人数为ξ,求Eξ.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:计算题,概率与统计
分析:(1)由分层抽样的特点,各层的比为5:6:2,共抽13人,即分别抽取男学生5人,女学生6人,教师2人,
设其中某项问题的选择,分别为“同意”、“不同意”两种,且每人都做了一种选择,即可完成表格;
(2)由(1)可得女生6人中有2人同意,男生5人中有3人同意,即可估计出高三年级学生“同意”的人数;
(3)由题意得ξ的取值为0,1,2,分别求出它们的概率注意分步相乘及古典概率的公式,再由期望公式,即可得到.
设其中某项问题的选择,分别为“同意”、“不同意”两种,且每人都做了一种选择,即可完成表格;
(2)由(1)可得女生6人中有2人同意,男生5人中有3人同意,即可估计出高三年级学生“同意”的人数;
(3)由题意得ξ的取值为0,1,2,分别求出它们的概率注意分步相乘及古典概率的公式,再由期望公式,即可得到.
解答:
解:(1)
(2)
×126+
×105=105(人);
(3)由题意得ξ的取值为0,1,2,
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,
∴Eξ=0×
+1×
+2×
=
.
则Eξ=
.
| 同意 | 不同意 | 合计 | |
| 教师 | 1 | 1 | 2 |
| 女学生 | 2 | 4 | 6 |
| 男学生 | 3 | 2 | 5 |
| 2 |
| 6 |
| 3 |
| 5 |
(3)由题意得ξ的取值为0,1,2,
P(ξ=0)=
| ||||
|
| 6 |
| 15 |
| ||||
|
| 8 |
| 15 |
| ||||
|
| 1 |
| 15 |
∴Eξ=0×
| 6 |
| 15 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
则Eξ=
| 2 |
| 3 |
点评:本题考查离散型随机变量的期望的求法,考查随机变量的概率的求法,注意运用两个计数原理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若奇函数f(x)在[2,5]上是增函数,且最小值是3,则它在[-5,-2]上是( )
| A、增函数且最小值是-3 |
| B、增函数且最大值是-3 |
| C、减函数且最大值是-3 |
| D、减函数且最小值是-3 |
给出下列说法:
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
双曲线
-
=1(b>0)的焦距为6,则双曲线的渐近线方程为( )
| x2 |
| 4 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
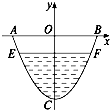 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.