题目内容
已知函数f(x)=x2-2x+4,其定义域为[a,a+1](a∈R).
(1)当a=1时,求f(x)的值域;
(2)设f(x)的值域为B,若7∈B,求f(x)的最小值.
(1)当a=1时,求f(x)的值域;
(2)设f(x)的值域为B,若7∈B,求f(x)的最小值.
考点:二次函数在闭区间上的最值,函数的定义域及其求法,函数的值域
专题:函数的性质及应用
分析:(1)对f(x)进行配方得f(x)=(x-1)2+3,a=1时,定义域为[1,2],通过解析式即可求出f(x)的值域;
(2)因为7∈B,所以x2-2x+4=7,解得x=-1,或3,所以-1∈[a,a+1],或3∈[a,a+1].-1∈[a,a+1]时,a≤-1≤a+1,能得到-1≤a+1≤0,所以f(x)在[a,a+1]上单调递减,所以x=a+1时,f(x)取最小值x2+3,同样的方法,当3∈[a,a+1]时,f(x)的最小值求出是a2-2a+4.
(2)因为7∈B,所以x2-2x+4=7,解得x=-1,或3,所以-1∈[a,a+1],或3∈[a,a+1].-1∈[a,a+1]时,a≤-1≤a+1,能得到-1≤a+1≤0,所以f(x)在[a,a+1]上单调递减,所以x=a+1时,f(x)取最小值x2+3,同样的方法,当3∈[a,a+1]时,f(x)的最小值求出是a2-2a+4.
解答:
解:(1)a=1时,f(x)的定义域为[1,2];
f(x)=x2-2x+4=(x-1)2+3,∴f(x)在[1,2]上单调递增;
∴f(x)的值域为[f(1),f(2)]=[3,4];
(2)解x2-2x+4=7得x=-1或3;
∵f(x)的定义域为[a,a+1];
∴-1∈[a,a+1],或3∈[a,a+1];
当-1∈[a,a+1]时,a≤-1≤a+1,∴-2≤a≤-1,-1≤a+1≤0;
∴f(x)在[a,a+1]上单调递减,x=a+1时,f(x)取最小值a2+3;
当3∈[a,a+1]时,a≤3≤a+1,∴2≤a≤3;
∴f(x)在[a,a+1]上单调递增;
∴x=a时,f(x)取最小值a2-2a+4.
f(x)=x2-2x+4=(x-1)2+3,∴f(x)在[1,2]上单调递增;
∴f(x)的值域为[f(1),f(2)]=[3,4];
(2)解x2-2x+4=7得x=-1或3;
∵f(x)的定义域为[a,a+1];
∴-1∈[a,a+1],或3∈[a,a+1];
当-1∈[a,a+1]时,a≤-1≤a+1,∴-2≤a≤-1,-1≤a+1≤0;
∴f(x)在[a,a+1]上单调递减,x=a+1时,f(x)取最小值a2+3;
当3∈[a,a+1]时,a≤3≤a+1,∴2≤a≤3;
∴f(x)在[a,a+1]上单调递增;
∴x=a时,f(x)取最小值a2-2a+4.
点评:考查对二次函数配方,根据二次函数的单调性求二次函数的值域,以及根据二次函数的单调性求二次函数的最值.

练习册系列答案
相关题目
函数y=x2cosx的导数为( )
| A、y′=x2cosx-2xsinx |
| B、y′=2xcosx+x2sinx |
| C、y′=2xcosx-x2sinx |
| D、y′=xcosx-x2sinx |
已知向量
=(1,x),
=(x,3),若
∥
,则|
|=( )
| a |
| b |
| a |
| b |
| a |
| A、1 | ||
B、
| ||
| C、4 | ||
| D、2 |




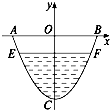 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.