题目内容
在△ABC中，内角A、B、C的对边分别为a、b、c，若
=
，则
=（ ）
| cosA-2cosC |
| cosB |
| 2c-a |
| b |
| sinC |
| sinA |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点：正弦定理,余弦定理
专题：解三角形
分析：由条件利用正弦定理可得sinBcosA+cosBsinA=2（sinBcosC+cosBsinC），再利用诱导公式、两角和的正弦公式求得
=的值．
| sinC |
| sinA |
解答：
解：在△ABC中，由
=
利用正弦定理可得
=
，
∴sinBcosA-2cosCsinB=2sinCcosB-sinAcosB，
∴sinBcosA+cosBsinA=2（sinBcosC+cosBsinC），
∴sin（B+A）=2sin（B+C），即 sinC=2sinA，则
=2，
故选：D．
| cosA-2cosC |
| cosB |
| 2c-a |
| b |
| cosA-2cosC |
| cosB |
| 2sinC-sinA |
| sinB |
∴sinBcosA-2cosCsinB=2sinCcosB-sinAcosB，
∴sinBcosA+cosBsinA=2（sinBcosC+cosBsinC），
∴sin（B+A）=2sin（B+C），即 sinC=2sinA，则
| sinC |
| sinA |
故选：D．
点评：本题主要考查正弦定理、诱导公式、两角和的正弦公式的应用，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
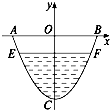一水渠的横截面如图所示，它的横截面曲线是抛物线形，AB宽2m，渠OC深为1.5m，水面EF距AB为0.5m．