题目内容
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)解关于x的不等式g(x)≥f(x)-|x-1|;
(2)如果对任意的x∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围.
(1)解关于x的不等式g(x)≥f(x)-|x-1|;
(2)如果对任意的x∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围.
考点:绝对值不等式的解法,函数恒成立问题
专题:不等式的解法及应用
分析:(1)不等式可化为 2x2-|x-1|≤0,分类讨论,却掉绝对值,求出不等式的解集.
(2)由题意可得c≤2x2 -|x-1|恒成立,令函数F(x)=
,分类讨论求得F(x)的最小值,可得实数c的取值范围.
(2)由题意可得c≤2x2 -|x-1|恒成立,令函数F(x)=
|
解答:
解:(1)由题意可得,g(x)和f(x)互为反函数,故g(x)=-x2+2x,
故不等式g(x)≥f(x)-|x-1|,即-x2+2x≥x2+2x-|x-1|,即2x2 ≤|x-1|,
∴x-1≥2x2 ①,或x-1≤-2x2 ②,解①求得x∈∅;解②求得-1≤x≤
.
综上可得,要求的不等式的解集为[-1,
].
(2)由题意可得-x2+2x+c≤x2+2x-|x-1|恒成立,即c≤2x2 -|x-1|恒成立.
令函数F(x)=
,∴当x≥1时,F(x)min=F(1)=2;
当x<1时,Fmin(x)=F(-
)=-
,
综上,可得函数F(x)的最小值为-
,
所以,实数c的取值范围是(-∞,-
].
故不等式g(x)≥f(x)-|x-1|,即-x2+2x≥x2+2x-|x-1|,即2x2 ≤|x-1|,
∴x-1≥2x2 ①,或x-1≤-2x2 ②,解①求得x∈∅;解②求得-1≤x≤
| 1 |
| 2 |
综上可得,要求的不等式的解集为[-1,
| 1 |
| 2 |
(2)由题意可得-x2+2x+c≤x2+2x-|x-1|恒成立,即c≤2x2 -|x-1|恒成立.
令函数F(x)=
|
当x<1时,Fmin(x)=F(-
| 1 |
| 4 |
| 9 |
| 8 |
综上,可得函数F(x)的最小值为-
| 9 |
| 8 |
所以,实数c的取值范围是(-∞,-
| 9 |
| 8 |
点评:本题考查求函数的解析式的方法以及解绝对值不等式的方法,体现了分类讨论的数学思想.

练习册系列答案
相关题目
若奇函数f(x)在[2,5]上是增函数,且最小值是3,则它在[-5,-2]上是( )
| A、增函数且最小值是-3 |
| B、增函数且最大值是-3 |
| C、减函数且最大值是-3 |
| D、减函数且最小值是-3 |
给出下列说法:
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
数列{an}中,a1=2,an+1=an+cn(c是常数),且a1,a2,a3成公比不为1的等比数列,则{an}的通项公式为( )
| A、n2+2n-1 |
| B、n2-2n+1 |
| C、n2+n |
| D、n2-n+2 |
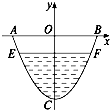 一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.
一水渠的横截面如图所示,它的横截面曲线是抛物线形,AB宽2m,渠OC深为1.5m,水面EF距AB为0.5m.