题目内容
已知平面a外两点A、B到平面a的距离分别为1和2，A、B两点在平面a内的射影之间的距离为
，求直线AB和平面a所成的角．
| 3 |
考点：直线与平面所成的角
专题：计算题,空间角
分析：根据线面所成角的定义，利用直角三角形的三角函数的定义加以计算，可得AB所在的直线和平面α所成的角．
解答：
解：设AB所在的直线和平面α所成的角是θ，
∵平面a外两点A、B到平面a的距离分别为1和2，A、B两点在平面a内的射影之间的距离为
，
∴可得tanθ=
结合θ∈[0，π]，可得θ=
即AB所在的直线和平面α所成的角为
．
∵平面a外两点A、B到平面a的距离分别为1和2，A、B两点在平面a内的射影之间的距离为
| 3 |
∴可得tanθ=
| 1 | ||
|
结合θ∈[0，π]，可得θ=
| π |
| 6 |
即AB所在的直线和平面α所成的角为
| π |
| 6 |
点评：本题着重考查了直线与平面所成角的定义和直角三角形中三角函数的定义等知识，属于中档题．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
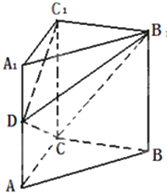如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，2AC=AA1=BC=2，D为棱AA1上的点．