题目内容
已知直线:x-y+m=0与双曲线x2-
=1交于不同的两点A、B,若线段AB的中点在圆x2+y2=5上,则m的值是 .
| y2 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:联立直线方程和双曲线方程,化为关于x的一元二次方程,由根与系数关系求得线段AB的中点,代入圆x2+y2=5求得m的值.
解答:
解:联立
,消y得 x2-2mx-m2-2=0,
△=4m2+4(m2+2)=8(m2+1)>0,
∵x1+x2=2m,
∴AB中点的横坐标为
=m,
代入x-y+m=0,得AB中点的纵坐标为2m.
∴AB中点(m,2m),
代入圆方程x2+y2=5,得m2+4m2=5,
∴m=±1.
故答案为:±1.
|
△=4m2+4(m2+2)=8(m2+1)>0,
∵x1+x2=2m,
∴AB中点的横坐标为
| 2m |
| 2 |
代入x-y+m=0,得AB中点的纵坐标为2m.
∴AB中点(m,2m),
代入圆方程x2+y2=5,得m2+4m2=5,
∴m=±1.
故答案为:±1.
点评:本题考查了双曲线的简单几何性质,考查了中点坐标公式的应用,是基础题.

练习册系列答案
相关题目
l是平面α外一条直线,过l作平面β,使α∥β,这样的β( )
| A、只能作一个 |
| B、至少可以做一个 |
| C、不存在 |
| D、至多可以作一个 |
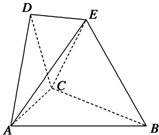 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.