题目内容
在△ABC中,已知向量
=(sinA-sinB,sinC),
=(
sinA-sinC,sinA+sinB),且
∥
,则角B= .
| m |
| n |
| 2 |
| m |
| n |
考点:两角和与差的正弦函数,平行向量与共线向量
专题:三角函数的求值
分析:根据向量共线的坐标条件列出方程,由正弦定理得到边的关系,再由余弦定理求出cosB,进而角B.
解答:
解:由题意得,
∥
,
所以(sinA-sinB)(sinA+sinB)-sinC(
sinA-sinC)=0,
sin2A-sin2B-
sinAsinC+sin2C=0,
由正弦定理得,a2-b2-
ac+c2=0,
即a2+c2-b2=
ac,
由余弦定理得,cosB=
=
又0<B<π,则B=45°,
故答案为:45°.
| m |
| n |
所以(sinA-sinB)(sinA+sinB)-sinC(
| 2 |
sin2A-sin2B-
| 2 |
由正弦定理得,a2-b2-
| 2 |
即a2+c2-b2=
| 2 |
由余弦定理得,cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
又0<B<π,则B=45°,
故答案为:45°.
点评:本题考查向量共线的坐标条件,以及正弦定理、余弦定理的应用,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
数列{an}的通项公式an=
(n∈N*),若前n项和为Sn,则Sn为( )
| 1 | ||||
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
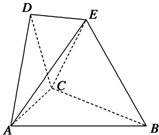 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.