题目内容
已知x,y之间的一组数据:
则y与x的线性回归方程
=bx+a必过点( )
| x | 2 | 4 | 6 | 8 |
| y | 1 | 5 | 3 | 7 |
 |
| y |
| A、(20,16) |
| B、(16,20) |
| C、(4,5) |
| D、(5,4) |
考点:线性回归方程
专题:计算题,概率与统计
分析:要求y与x的线性回归方程为y=bx+a必过的点,需要先求出这组数据的样本中心点,根据所给的表格中的数据,求出横标和纵标的平均值,得到样本中心点,得到结果.
解答:
解:∵
=
=5,
=
=4,
∴本组数据的样本中心点是(5,4),
∴y与x的线性回归方程为y=bx+a必过点(5,4)
故选D.
. |
| x |
| 2+4+6+8 |
| 4 |
. |
| y |
| 1+5+3+7 |
| 4 |
∴本组数据的样本中心点是(5,4),
∴y与x的线性回归方程为y=bx+a必过点(5,4)
故选D.
点评:本题考查平均值的计算方法,回归直线的性质:回归直线方程一定过样本的中心点

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
计算:[(-
)2]-1=( )
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
设函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-4或2 | B、-4或-2 |
| C、-2或4 | D、-2或2 |
若m,n是正整数,则m+n>mn成立的充要条件是( )
| A、m,n都等于1 |
| B、m,n都不等于2 |
| C、m,n都大于1 |
| D、m,n至少有一个等于1 |
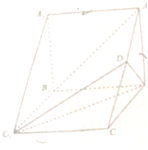 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.