题目内容
计算:[(-
)2]-1=( )
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:根据指数幂的公式进行化简即可.
解答:
解:[(-
)2]-1=[(
)2]-1=2-1=
,
故选:B
| 2 |
| 2 |
| 1 |
| 2 |
故选:B
点评:本题主要考查有理数的化简,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,不具有奇偶性的函数是( )
| A、y=ex-e-x | ||
B、y=lg
| ||
| C、y=cos2x | ||
| D、y=sinx+cosx |
已知函数f(x)=
且f′(1)=2,则实数a的值为( )
| ax2-1 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、a>0 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A、y=cosx | ||
| B、y=ln|x| | ||
C、y=
| ||
| D、y=tan2x |
已知x,y之间的一组数据:
则y与x的线性回归方程
=bx+a必过点( )
| x | 2 | 4 | 6 | 8 |
| y | 1 | 5 | 3 | 7 |
 |
| y |
| A、(20,16) |
| B、(16,20) |
| C、(4,5) |
| D、(5,4) |
已知向量
=(cosθ,sinθ),
=(1,-2),若
∥
,则代数式
的值是( )
| a |
| b |
| a |
| b |
| 2sinθ-cosθ |
| sinθ+cosθ |
A、
| ||
B、
| ||
| C、5 | ||
D、
|
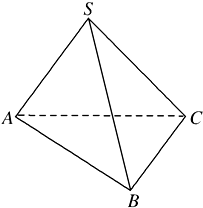 如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是
如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是