题目内容
12.设函数f(x)=(x+k+1)$\sqrt{x-k}$,g(x)=$\sqrt{x-k+3}$,其中k是实数.(1)若k=0,解不等式$\sqrt{x}$•f(x)≥$\frac{1}{2}$$\sqrt{x+3}$•g(x);
(2)若k≥0,求关于x的方程f(x)=x•g(x)实根的个数.
分析 (1)若k=0,先化简不等式即可解不等式$\sqrt{x}$•f(x)≥$\frac{1}{2}$$\sqrt{x+3}$•g(x);
(2)若k≥0,化简方程f(x)=x•g(x),然后讨论k的取值范围即可得到结论.
解答 解:(1)若k=0,f(x)=(x+1)$\sqrt{x}$,g(x)=$\sqrt{x+3}$,
则不等式$\sqrt{x}$•f(x)≥$\frac{1}{2}$$\sqrt{x+3}$•g(x)等价为$\sqrt{x}$•(x+1)$\sqrt{x}$≥$\frac{1}{2}$$\sqrt{x+3}$•$\sqrt{x+3}$,
此时$\left\{\begin{array}{l}{x≥0}\\{x+3≥0}\end{array}\right.$,即x≥0,
此时不等式等价为(x+1)x≥$\frac{1}{2}$(x+3),
即2x2+x-3≥0,得x≥1或x≤-$\frac{3}{2}$,
∵x≥0,∴x≥1,即不等式的解集为[1,+∞).
(2)若k≥0,由f(x)=x•g(x)得(x+k+1)$\sqrt{x-k}$=x$\sqrt{x-k+3}$,①.
由$\left\{\begin{array}{l}{x-k≥0}\\{x-k+3≥0}\end{array}\right.$得$\left\{\begin{array}{l}{x≥k}\\{x≥k-3}\end{array}\right.$,即x≥k,∴当x≥0时x-k+1>0,
方程①两边平方整理得(2k-1)x2-(k2-1)x-k(k+1)2=0,(x≥k),②
当k=$\frac{1}{2}$时,由②得x=$\frac{3}{2}$,∴方程有唯一解,
当k≠$\frac{1}{2}$时,由②得判别式△=(k+1)2(3k-1)2,
1)当k=$\frac{1}{3}$时,判别式△=0,方程②有两个相等的根x=$\frac{4}{3}$$>\frac{1}{3}$,∴原方程有唯一解.
2)0≤k<$\frac{1}{2}$且k≠$\frac{1}{3}$时,方程②整理为[(2k-1)x+k(k+1)](x-k-1)=0,
解得x1=$\frac{k(k+1)}{1-2k}$,x2=k+1,
由于判别式△>0,∴x1≠x2,其中x2=k+1>k,x1-k=$\frac{3{k}^{2}}{1-2k}$≥0,即x1≥k,
故原方程有两解,
3)当k>$\frac{1}{2}$时,由2)知,x1-k=$\frac{3{k}^{2}}{1-2k}$<0,即x1<k,故x1不是原方程的解,而x2=k+1>k,则原方程有唯一解,
综上所述,当k≥$\frac{1}{2}$或k=$\frac{1}{3}$时,原方程有唯一解,
当0≤k<$\frac{1}{2}$且k≠$\frac{1}{3}$时,原方程有两解.
点评 本题主要考查不等式的求解以及方程根的个数的判断,综合性较强,难度较大,考查学生的分类讨论的数学思想.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案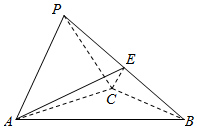 如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.
如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.(Ⅰ)求证:AP⊥PC;
(Ⅱ)若PC=1,求三棱锥A-PEC的体积.
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{4}$ |
| A. | 3或$\frac{7}{3}$ | B. | $\frac{7}{3}$ | C. | 3 | D. | 3或$-\frac{10}{3}$ |
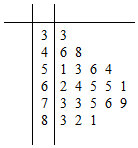 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |