题目内容
4.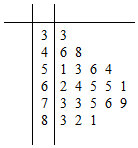 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
分析 (Ⅰ)根据茎叶图,填写2×2列联表,计算出K2的值,对照数表得出结论;
(Ⅱ)利用频率值估计概率即可;
(Ⅲ)用列举法计算基本事件数,求出对应的概率即可.
解答 解:(Ⅰ)根据茎叶图,填写2×2列联表,如下;
| 不满意 | 满意 | 合计 | |
| 男 | 3 | 4 | 7 |
| 女 | 11 | 2 | 13 |
| 合计 | 14 | 6 | 20 |
∵K2≈3.7781<3.84 1,
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关;----(4分)
(Ⅱ)因样本20人中,对该公司产品满意的有6人,
故估计用户对该公司的产品“满意”的概率为$\frac{6}{20}=0.3$,----(6分)
(Ⅲ)由(Ⅰ)知,对该公司产品满意的用户有6人,其中男用户4人,女用户2人,
设男用户分别为a,b,c,d;女用户分别为e,f,----(8分)
从中任选两人,记事件A为“选取的两个人都是男用户或都是女用户”,则
总的基本事件为(a,b),(a,c),(a,d),(a,e),(a,f),
(b,c),(b,d),(b,e),(b,f),
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15个,----(10分)
而事件A包含的基本事件为(a,b),(a,c),(a,d),
(b,c),(b,d),(c,d),(e,f)共7个,
故P(A)=$\frac{7}{15}$.--(12分)
点评 本题主要考查茎叶图与对立性检验的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
14.设O是△ABC的外接圆圆心,且$\overrightarrow{OA}+\sqrt{3}\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$,则∠AOC=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
13.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-2y+4≥0}\\{2x-y-4≤0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | $\frac{11}{3}$ | B. | 5 | C. | $\frac{16}{3}$ | D. | 12 |
14.将函数f(x)=sin(2x+$\frac{π}{6}$)图象上所有点向右平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则y=g(x)的图象的一条对称轴是直线( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{2π}{3}$ |