题目内容
20.从集合A={-2,-1,2}中随机选取一个数记为a,从集合B={-1,1,3}中随机选取一个数记为b,则直线ax-y+b=0不经过第四象限的概率为( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{4}$ |
分析 本题是一个古典概型,试验发生包含的事件(a,b)的取值所有可能的结果可以列举出,满足条件的事件直线不经过第四象限,符合条件的(a,b)有2种结果,根据古典概型概率公式得到结果.
解答 解:由题意知本题是一个古典概型,试验发生包含的事件a∈A={-2,-1,1},b∈B={-1,1,3},
得到(a,b)的取值所有可能的结果有:
(-2,-1);(-2,1);(-2,3);(-1,-1);(-1,1);(-1,3);(2,-1);(2,1);(2,3)共9种结果.
由ax-y+b=0得y=ax+b,当$\left\{\begin{array}{l}{a>0}\\{b≥0}\end{array}\right.$时,直线不经过第四限,符合条件的(a,b)有(2,1);(2,3),2种结果,
∴直线不过第四象限的概率P=$\frac{2}{9}$,
故选:A.
点评 本题主要考查古典概型的概率的计算,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、体积的比值得到,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.已知函数f(x)满足f(x)+f(2-x)=2,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,$f(x)+2=\frac{2}{{f(\sqrt{x+1})}}$,若定义在(-1,3)上的函数g(x)=f(x)-t(x+1)有三个不同的零点,则实数t的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
8.平面直角坐标系xOy中,已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$关于y轴对称,向量$\overrightarrow{a}$=(1,0),则满足$\overrightarrow{O{A}^{2}}$+$\overrightarrow{a}$$•\overrightarrow{AB}$=0的点A(x,y)的轨迹方程为( )
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
5.若程序框图如图所示,则该程序运行后输出k的值是( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
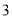 ,且每个顶点都在球
,且每个顶点都在球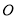 的表面上,则球
的表面上,则球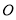 的半径为( )
的半径为( )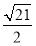 B.
B.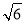 C.
C.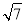 D.
D.