题目内容
7.二项式${(ax-\frac{{\sqrt{3}}}{6})^3}$(a>0)的展开式的第二项的系数为-$\frac{{\sqrt{3}}}{2}$,则$\int_{-2}^a{x^2}$dx的值为( )| A. | 3或$\frac{7}{3}$ | B. | $\frac{7}{3}$ | C. | 3 | D. | 3或$-\frac{10}{3}$ |
分析 二项式${(ax-\frac{{\sqrt{3}}}{6})^3}$(a>0)的展开式的通项公式T2=${∁}_{3}^{1}(ax)^{2}(-\frac{\sqrt{3}}{6})$=$-\frac{\sqrt{3}}{2}$a2x2.由于第二项的系数为-$\frac{{\sqrt{3}}}{2}$,可得$-\frac{\sqrt{3}}{2}{a}^{2}$=-$\frac{\sqrt{3}}{2}$,即a2=1,解得a,再利用微积分基本定理即可得出.
解答 解:二项式${(ax-\frac{{\sqrt{3}}}{6})^3}$(a>0)的展开式的通项公式T2=${∁}_{3}^{1}(ax)^{2}(-\frac{\sqrt{3}}{6})$=$-\frac{\sqrt{3}}{2}$a2x2.
∵第二项的系数为-$\frac{{\sqrt{3}}}{2}$,
∴$-\frac{\sqrt{3}}{2}{a}^{2}$=-$\frac{\sqrt{3}}{2}$,
∴a2=1,a>0,解得a=1.
当a=1时,则$\int_{-2}^a{x^2}$dx=${∫}_{-2}^{1}{x}^{2}dx$=$\frac{{x}^{3}}{3}{|}_{-2}^{1}$=3.
故选:C.
点评 本题考查了二项式定理与微积分基本定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
18.已知A与B是两个事件,P(B)=$\frac{1}{4}$,P(AB)=$\frac{1}{8}$,则P(A|B)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
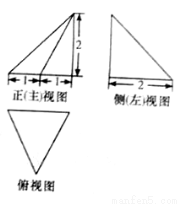
 B.
B. C.
C.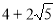 D.
D.
 如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.
如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.