题目内容
3.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x|,x<1}\\{{{(x-1)}^2},x>1}\end{array}}\right.$,若方程f2(x)+af(x)+b=0有五个不同的根,则a的取值范围为(-2,-1).分析 设t=f(x),作出函数f(x)的图象,根据数形结合以及方程根的关系进行判断求解即可.
解答 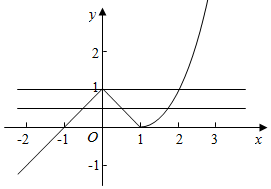 解:设t=f(x),
解:设t=f(x),
作出函数f(x)的图象如图
则当t=1时,t=f(x)有两个根,
当t>1或t≤0时,t=f(x)有一个根,
当0<t<1时,t=f(x)有3个根,
若方程f2(x)+af(x)+b=0有五个不同的根,
则等价为方程t2+at+b=0有两个不同的根,t1=1或0<t2<1,
则1<t1+t2<2,
即1<-a<2,则-2<a<-1,
即a的取值范围为(-2,-1),
故答案为:(-2,-1).
点评 本题主要考查函数与方程的应用,利用换元法结合数形结合以及函数图象的关系建立不等式关系是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
14.设O是△ABC的外接圆圆心,且$\overrightarrow{OA}+\sqrt{3}\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$,则∠AOC=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
11.已知函数f(x)满足f(x)+f(2-x)=2,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,$f(x)+2=\frac{2}{{f(\sqrt{x+1})}}$,若定义在(-1,3)上的函数g(x)=f(x)-t(x+1)有三个不同的零点,则实数t的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
18.已知A与B是两个事件,P(B)=$\frac{1}{4}$,P(AB)=$\frac{1}{8}$,则P(A|B)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
8.平面直角坐标系xOy中,已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$关于y轴对称,向量$\overrightarrow{a}$=(1,0),则满足$\overrightarrow{O{A}^{2}}$+$\overrightarrow{a}$$•\overrightarrow{AB}$=0的点A(x,y)的轨迹方程为( )
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
13.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-2y+4≥0}\\{2x-y-4≤0}\end{array}\right.$,则z=2x+y的最大值为( )
| A. | $\frac{11}{3}$ | B. | 5 | C. | $\frac{16}{3}$ | D. | 12 |