题目内容
2.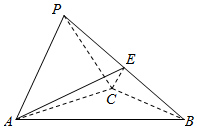 如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.
如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.(Ⅰ)求证:AP⊥PC;
(Ⅱ)若PC=1,求三棱锥A-PEC的体积.
分析 (Ⅰ)在△ACB中,利用已知结合勾股定理可得AC⊥BC,再由面面垂直的性质可得BC⊥PA,由线面垂直的判定得PA⊥面PBC,则有AP⊥PC;
(Ⅱ)求解直角三角形可得三角形PCB的面积,结合E为PB边的中点得三角形PCE的面积,再求解直角三角形求得PA,代入棱锥体积公式求得三棱锥A-PEC的体积.
解答 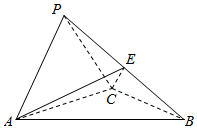 (Ⅰ)证明:如图,在△ACB中
(Ⅰ)证明:如图,在△ACB中
∵AC=BC=2,AB=2$\sqrt{2}$,∴AC2+BC2=AB2,则AC⊥BC,
又侧面PAC⊥底面ABC,∴BC⊥面PAC,则BC⊥PA,
又AP⊥PB,且PB∩BC=B,
∴PA⊥面PBC,则AP⊥PC;
(Ⅱ)解:在Rt△PCB中,由PC=1,BC=2,
可得${S}_{△PBC}=\frac{1}{2}×1×2=1$,
∵E为PB边的中点,∴${S}_{△PEC}=\frac{1}{2}{S}_{△PBC}=\frac{1}{2}$,
在Rt△APC中,
由PC=1,AC=2,得$PA=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
∴${V}_{A-PEC}=\frac{1}{3}×\frac{1}{2}×PA$=$\frac{\sqrt{3}}{6}$.
点评 本题考查平面与平面垂直的判定,考查了三棱锥体积的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
14.设O是△ABC的外接圆圆心,且$\overrightarrow{OA}+\sqrt{3}\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$,则∠AOC=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
11.已知函数f(x)满足f(x)+f(2-x)=2,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,$f(x)+2=\frac{2}{{f(\sqrt{x+1})}}$,若定义在(-1,3)上的函数g(x)=f(x)-t(x+1)有三个不同的零点,则实数t的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
 ,且每个顶点都在球
,且每个顶点都在球 的表面上,则球
的表面上,则球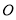 的半径为( )
的半径为( )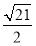 B.
B.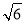 C.
C.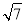 D.
D.
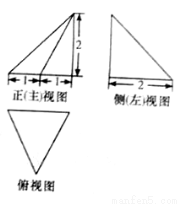
 B.
B. C.
C.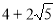 D.
D.
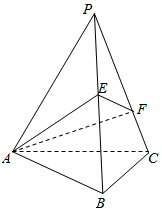 如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.
如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.