题目内容
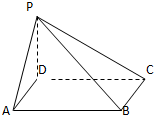 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=| 2 |
(1)求证:PD⊥平面ABCD;
(2)求二面角P-BC-D的大小.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知推导出PD⊥AD,同理PD⊥CD,由此能证明PD⊥底面ABCD.
(2)由PD⊥面ABCD,得二面角P-BC-D为∠PCD,由此能求出二面角P-BC-D的大小.
(2)由PD⊥面ABCD,得二面角P-BC-D为∠PCD,由此能求出二面角P-BC-D的大小.
解答:
(1)证明:因为四棱锥P-ABCD,底面是边长为a的正方形,
侧棱PD=a,PA=PC=
a,
即PA2=2a2=DA2+PD2=a2+a2,
所以PD⊥AD,同理PD⊥CD,AD∩CD=D,
所以PD⊥底面ABCD.
(2)因为PD⊥面ABCD,
所以二面角P-BC-D的平面角为∠PCD,
因为PD=a,DC=a,PD⊥DC,
所以,∠PCD=45°,
所以二面角P-BC-D为45°.
侧棱PD=a,PA=PC=
| 2 |
即PA2=2a2=DA2+PD2=a2+a2,
所以PD⊥AD,同理PD⊥CD,AD∩CD=D,
所以PD⊥底面ABCD.
(2)因为PD⊥面ABCD,
所以二面角P-BC-D的平面角为∠PCD,
因为PD=a,DC=a,PD⊥DC,
所以,∠PCD=45°,
所以二面角P-BC-D为45°.
点评:本题考查直线与平面垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
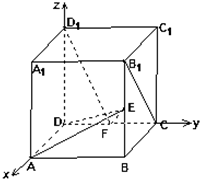 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点, 如图,在正方形ABCD中,点P是△BCD内部或边界上任一点,设
如图,在正方形ABCD中,点P是△BCD内部或边界上任一点,设