题目内容
定义在R上的奇函数f(x)满足f(x)=f(x+4),且x∈(0,2]时,f(x)=
.
(1)求f(x)在[-2,2]上的解析式;
(2)判断f(x)在[0,2]上的单调性,并给予证明;
(3)当λ为何值时,关于方程f(x)=λ在[-2,2]上有实数解?
| 3x |
| 3x+1 |
(1)求f(x)在[-2,2]上的解析式;
(2)判断f(x)在[0,2]上的单调性,并给予证明;
(3)当λ为何值时,关于方程f(x)=λ在[-2,2]上有实数解?
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)由条件可得函数的周期为4,设x∈[-2,0),则-x∈(0,2],根据f(-x)=
=
=-f(x),求得f(x)=
.再根据奇函数的定义可得f(0)=0,从而求得可得,f(x)在[-2,2]上的解析式.
(2)根据f(0)=0,当x∈(0,2]时,由于f(x)=1-
>0,且f(x)随着x的增大而增大,可得f(x)在[0,2]上是增函数.再利用函数的单调性的定义进行证明.
(3)由题意可得,本题即求函数λ=f(x)在[-2,2]上的值域,再利用函数的单调性求得函数f(x)在[-2,2]上的值域.
| 3-x |
| 3-x+1 |
| 1 |
| 1+3x |
| -1 |
| 1+3x |
(2)根据f(0)=0,当x∈(0,2]时,由于f(x)=1-
| 1 |
| 3x+1 |
(3)由题意可得,本题即求函数λ=f(x)在[-2,2]上的值域,再利用函数的单调性求得函数f(x)在[-2,2]上的值域.
解答:
解:(1)∵奇函数f(x)满足f(x)=f(x+4),故函数的周期为4.
由于x∈(0,2]时,f(x)=
,设x∈[-2,0),则-x∈(0,2],故 f(-x)=
=
=-f(x),
∴f(x)=
.
再根据奇函数的定义可得f(0)=0,可得,f(x)在[-2,2]上的解析式为f(x)=
.
(2)在[0,2]上,f(0)=0,当x∈(0,2]时,由于f(x)=
=1-
>0,
且f(x)随着x的增大而增大,故f(x)在[0,2]上是增函数.
证明:设0≤x1<x2≤2,则由f(x1)-f(x2)=[1-
]-[1-
]=
<0,可得f(x1)<f(x2),
故f(x)在[0,2]上是增函数.
(3)由题意可得,本题即求函数λ=f(x)在[-2,2]上的值域.
利用函数的单调性求得函数f(x)在[-2,2]上的值域为 {λ|y=0,或
<λ≤
,或-
≤λ<-
},
故λ的范围为:{λ|y=0,或
<λ≤
,或-
≤λ<-
}.
由于x∈(0,2]时,f(x)=
| 3x |
| 3x+1 |
| 3-x |
| 3-x+1 |
| 1 |
| 1+3x |
∴f(x)=
| -1 |
| 1+3x |
再根据奇函数的定义可得f(0)=0,可得,f(x)在[-2,2]上的解析式为f(x)=
|
(2)在[0,2]上,f(0)=0,当x∈(0,2]时,由于f(x)=
| 3x |
| 3x+1 |
| 1 |
| 3x+1 |
且f(x)随着x的增大而增大,故f(x)在[0,2]上是增函数.
证明:设0≤x1<x2≤2,则由f(x1)-f(x2)=[1-
| 1 |
| 3x1 |
| 1 |
| 3x2 |
| 3x1-3x2 |
| 3x1•3x2 |
故f(x)在[0,2]上是增函数.
(3)由题意可得,本题即求函数λ=f(x)在[-2,2]上的值域.
利用函数的单调性求得函数f(x)在[-2,2]上的值域为 {λ|y=0,或
| 1 |
| 2 |
| 9 |
| 10 |
| 9 |
| 10 |
| 1 |
| 2 |
故λ的范围为:{λ|y=0,或
| 1 |
| 2 |
| 9 |
| 10 |
| 9 |
| 10 |
| 1 |
| 2 |
点评:本题主要考查函数的周期性、单调性和奇偶性的应用,求函数的解析式和函数的值域,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目

 y=sinx+2|sinx|.
y=sinx+2|sinx|.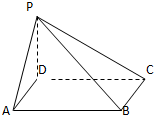 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=