题目内容
（理）设函数f（x）=sinx+cosx，f′（x）是f（x）的导数，若f（x）=2f′（x），则
= ．
| sin2x-sin2x |
| cos2x |
考点：导数的运算
专题：导数的概念及应用
分析：求出函数的导数，建立条件关系即可得到结论．
解答：
解：函数的导数为f′（x）=cosx-sinx，
∵f（x）=2f′（x），
∴sinx+cosx=2cosx-2sinx，
即3sinx=cosx，
则
=
=
=-
，
故答案为：-
∵f（x）=2f′（x），
∴sinx+cosx=2cosx-2sinx，
即3sinx=cosx，
则
| sin2x-sin2x |
| cos2x |
| sin2x-2sinxcosx |
| cos2x |
| sin2x-6sinx2x |
| 9sin2x |
| 5 |
| 9 |
故答案为：-
| 5 |
| 9 |
点评：本题主要考查导数的基本运算以及函数值的求解，求出函数的导数建立条件关系是解决本题的关键．
练习册系列答案
相关题目
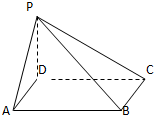如图，在四棱锥P-ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=