题目内容
在△ABC中,角A,B,C所对边分别为a,b,c,且c=4
,B=45°,面积S=2,则b等于 .
| 2 |
考点:余弦定理,正弦定理
专题:解三角形
分析:先利用面积公式和已知条件求得a,进而利用余弦定理求得b.
解答:
解:由余弦定理知cosB=
=
=
,
∴a2-b2=8a-32,①
∵S=
acsinB=
a•4
•
=2,
∴a=1,代入①得b=5,
故答案为5.
| a2+c2-b2 |
| 2ac |
| a2+32-b2 | ||
8
|
| ||
| 2 |
∴a2-b2=8a-32,①
∵S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴a=1,代入①得b=5,
故答案为5.
点评:本题主要考查了余弦定理和正弦定理的应用.解三角形问题中的边和角的问题常需要正弦定理和余弦定理结合,故应能灵活运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
设G是△ABC的重心,且(2tanA)
+(3tanB)
+
=
,则A+B=( )
| GA |
| GB |
| GC |
| 0 |
| A、45° | B、65° |
| C、135° | D、150° |
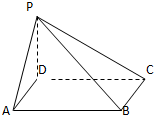 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=