题目内容
已知函数f(x)为R上的奇函数,且当x>0时,f(x)=
+1.
(1)用定义证明:f(x)在(0,+∞)上为增函数;
(2)求f(x)的解析式.
| x |
(1)用定义证明:f(x)在(0,+∞)上为增函数;
(2)求f(x)的解析式.
考点:函数单调性的判断与证明,函数解析式的求解及常用方法
专题:计算题,证明题,函数的性质及应用
分析:(1)定义法通常分五步;取值,作差,化简变形,判号,下结论;(2)利用奇函数求解析式.
解答:
解:(1)证明;任取x1、x2,且0<x1<x2,
则x1-x2<0,
+
>0
f(x1)-f(x2)=
-
=
<0
∴f(x1)<f(x2),
∴f(x)在(0,+∞)上为增函数.
(2)∵函数f(x)为R上的奇函数,
∴①当x=0时,f(0)=0;
②当x<0时,-x>0,
则f(x)=-f(-x)=-(
+1)=-
-1;
综上所述,f(x)=
.
则x1-x2<0,
| x1 |
| x2 |
f(x1)-f(x2)=
| x1 |
| x2 |
| x1-x2 | ||||
|
∴f(x1)<f(x2),
∴f(x)在(0,+∞)上为增函数.
(2)∵函数f(x)为R上的奇函数,
∴①当x=0时,f(0)=0;
②当x<0时,-x>0,
则f(x)=-f(-x)=-(
| -x |
| -x |
综上所述,f(x)=
|
点评:考查了定义法证明单调性的步骤:取值,作差,化简变形,判号,下结论;注意化简变形,相对较难;同时考查了利用奇偶性求函数解析式的方法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 y=sinx+2|sinx|.
y=sinx+2|sinx|.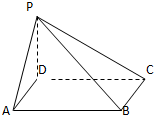 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=