题目内容
在△ABC中，内角A、B、C对边的边长分别是a，b，c，已知c=2，C=
．
（1）若△ABC的面积等于
，求a，b；
（2）若sin（A+C）=2sinA，求△ABC的面积．
| π |
| 3 |
（1）若△ABC的面积等于
| 3 |
（2）若sin（A+C）=2sinA，求△ABC的面积．
考点：余弦定理,正弦定理
专题：解三角形
分析：（1）先由余弦定理求得a和b的关系式，然后利用面积公式求得a和b的另一个关系式，进而联立求得a和b．
（2）利用正弦定理把角的正弦转化为边的关系，利用余弦定理进而求得a和b，最后利用三角形面积公式求得答案．
（2）利用正弦定理把角的正弦转化为边的关系，利用余弦定理进而求得a和b，最后利用三角形面积公式求得答案．
解答：
解：（1）由余弦定理c2=a2+b2-2abcosC，的a2+b2-ab=4，
又∵△ABC的面积等于
，
∴
absinC=
ab•
=
，
∴ab=4，
得a=b=2．
（2）sin（A+C）=2sinA，
∴sinB=2sinA，
∴b=2a，
∵a2+b2-ab=4，b=2a，
∴a=
，b=
，
∴S△ABC=
absinC=
．
又∵△ABC的面积等于
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴ab=4，
得a=b=2．
（2）sin（A+C）=2sinA，
∴sinB=2sinA，
∴b=2a，
∵a2+b2-ab=4，b=2a，
∴a=
2
| ||
| 3 |
4
| ||
| 3 |
∴S△ABC=
| 1 |
| 2 |
2
| ||
| 3 |
点评：本题主要考查了正弦定理和余弦定理的应用．考查了学生基础知识的掌握和一定的运算能力．
练习册系列答案
备战中考寒假系列答案
相关题目
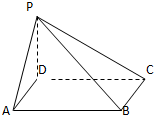如图，在四棱锥P-ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=